스탠포드 강의를 듣고 정리한 내용입니다.
지난 포스팅에서는 Relational Classification, Iterative Classification에 대해서 알아보았습니다.
이번 포스팅에서는 Belief Propgation에 대해서 알아보겠습니다.
Belief Propagation
지난 포스팅에서 설명한 방법론들을 살펴보면 모두 이웃 노드로부터 받은 확률의 가중 평균으로 자기 자신을 업데이트합니다. (초기에는 라벨로 부터 받죠) 이 말은 즉, 주변 노드가 현재 노드의 결정에 영향을 준다는 말이죠.

학교에서 쪽지 돌리는 것을 생각해보죠. 서로 가깝거나 연결된 사람에게 쪽지를 돌릴 수 있습니다. 이것을 이웃 노드가 belief를 준다 라고 표현합니다. 노드는 이웃 노드들로부터 belief를 받아 자신을 업데이트하고, 또 다른 주변 노드에게 업데이트된 belief를 전달합니다. 이렇게 계속 전달하다보면 멀리 있는 노드의 belief도 받을 수 있게 됩니다. 받는 것은 바로 이웃에게 받지만, 그 이웃은 또 이웃의 이웃에게 받아온 정보이기 때문이죠!
예시
몇 가지 예를 들어 보겠습니다. 첫 번째로는 일렬로 된 path graph입니다.

위의 그래프에 노드가 몇개인지 노드 간의 iteract(message passing)를 통해 세보도록 하죠! 시작 노드는 1입니다.

위와 같이 count용 변수를 m이라고 할 때, 각 노드는 받은 메세지에 1을 더하여 다음 노드로 넘겨줍니다. 이렇게 하면 마지막 노드에서 노드의 최종 개수를 알 수 있죠.
두 번째 예시는 트리 형태의 그래프입니다.
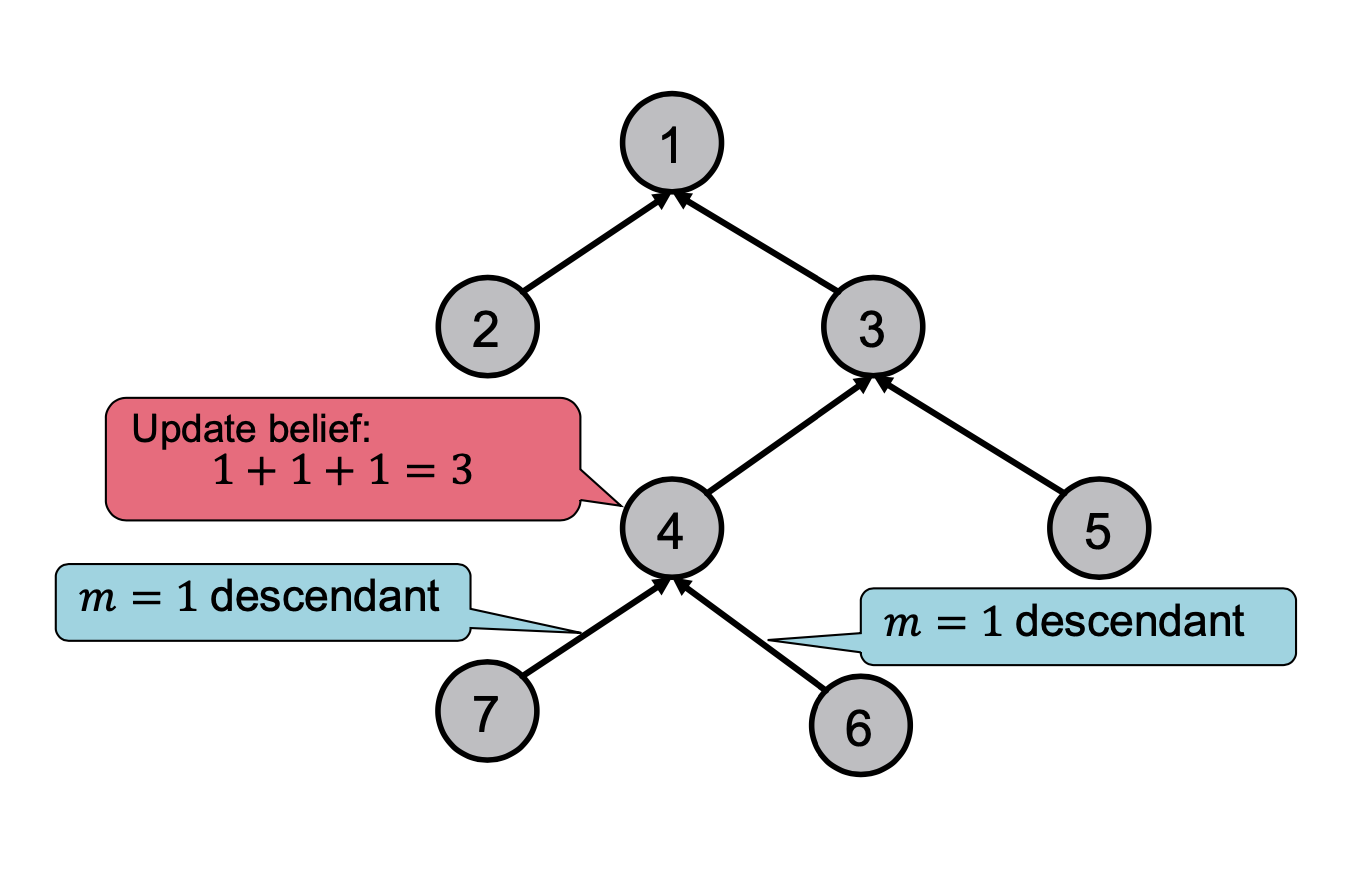
위의 그래프에서도 같은 목표를 가지고 있고, leaf 노드에서 root노드로 가면서 노드를 카운트 합니다.
각 노드는 자신의 leaf node로부터 받은 값을 모두 더하고, 자기 자신인 1을 더하여 다음 노드에게 전달해줍니다.

root노드까지 반복하면 위와 같이 노드 개수를 구할 수 있습니다.
전에도 언급했지만, 위의 예를 통해 다음 노드로 전달하는 것은 이전 노드로부터 받은 값이고, 노드가 어떤 값을 받았냐에 따라 전달하는 값은 변한다는 것을 알 수 있습니다.
지금까지는 각 노드들이 정보를 어떻게 전달하는지 간단한 예시로 확인해 보았습니다.
이제부터는 실제 알고리즘이 어떻게 되어있는지, 어떤 정보를 전달하는지 알아보겠습니다.
작동 과정
실제 어떻게 작동하는지 알기 전, 몇 가지 개념들을 정의하겠습니다.
- ψ : ψ(Yi, Yj)는 이웃 노드 i의 라벨이 Yi일 때, 노드 j가 Yj일 확률의 비중으로, 각 노드가 이웃 노드의 클래스에 대한 영향력을 행렬로 표현한 것
- ϕ : ϕ(Yi)는 노드 i가 라벨 Yi일 확률
- mi→j(Yj) : 노드 i의 메세지가 노드 j로 전달 되는 것
- L : 모든 라벨을 포함하는 집합
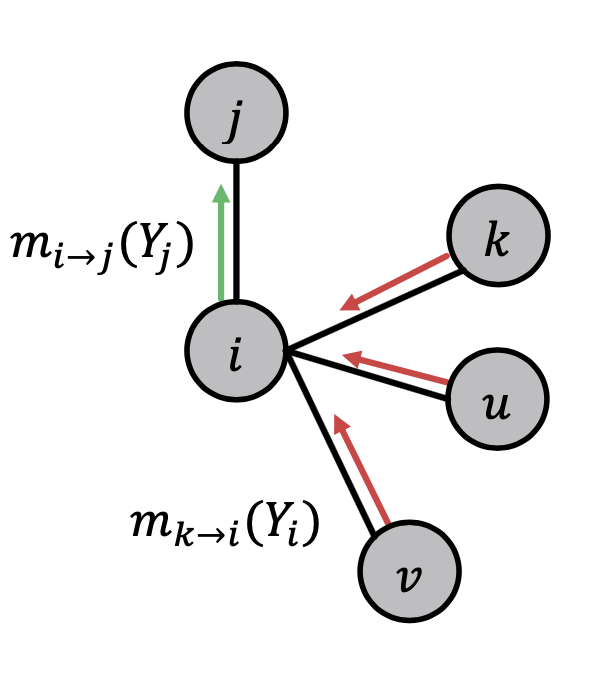
다음과 같은 그래프가 있다고 가정합시다.
현재 그래프의 목적은 기준 노드 i에서 부터 목적 노드 j까지 belief를 보내는 것입니다.
이를 위해서는 아래와 같은 과정들을 거칩니다.
1. 초기 모든 메세지는 1로 초기화
2. 노드 간의 메세지 전달을 계속 반복(아래 수식 참고)
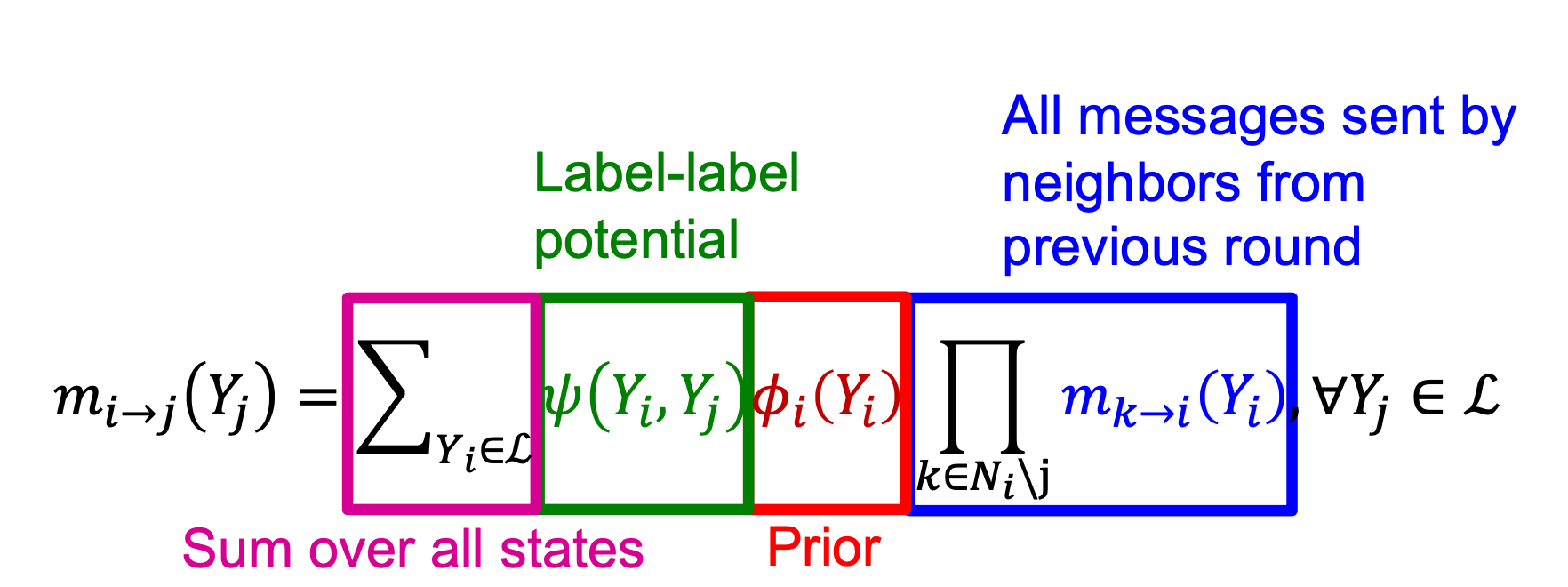
왼쪽 부터 오른쪽으로 수식을 설명하겠습니다.
분홍색
모든 종류의 라벨에 대해 현재 노드 i의 가능성을 측정
초록색
i노드의 각 라벨 마다 j노드가 Yj라벨을 가질 확률을 계산(쉽게 말하면 노드 i의 라벨에 따른 노드 j의 라벨 분포? 라고 생각하시면 될것같습니다. 왜냐하면 노드 j도 결국 이웃 노드인 노드 i의 영향을 받기 때문이죠.)
빨간색
i가 어떤 라벨을 가질지 확률을 계산해 줍니다.
파란색
기준 되는 노드(i)로 오는 모든 belief들을 모아줍니다.(노드 i가 Yi라벨일 belief를 넘겨받음)
빨간색
i가 어떤 라벨을 가질지 확률을 계산해 줍니다.
위의 수식을 반복하여 수렴한다면 아래와 같이 실제 확률이 계산됩니다.
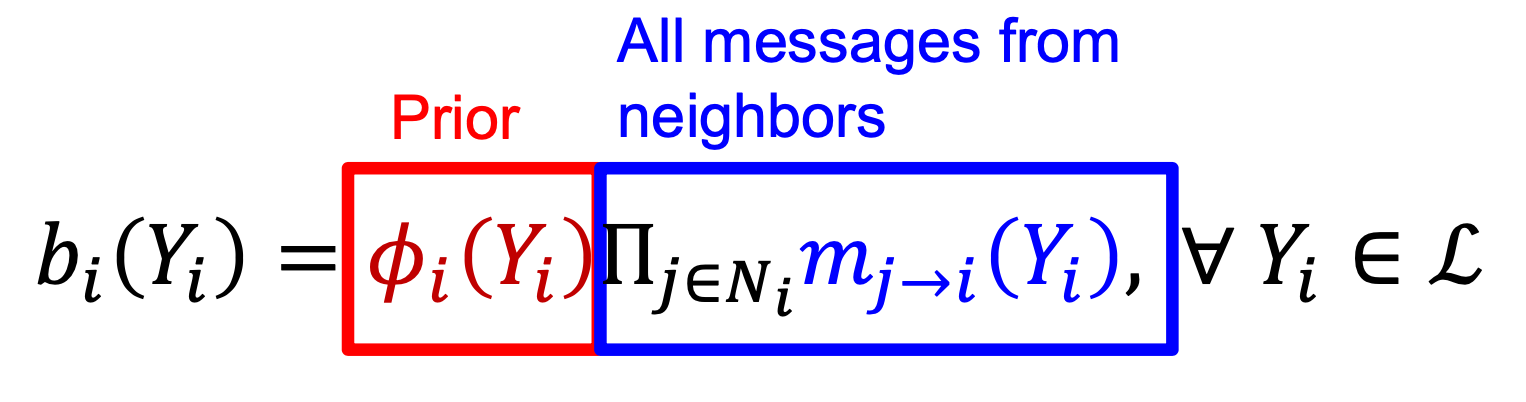
빨간색
노드 i가 라벨 Yi를 가질 확률
파란색
노드 i가 이웃 이웃 노드로부터 오는 모든 belief의 모음
수식을 설명해 보자면, bi(Yi)는 노드 i가 Yi일 확률과 노드 i의 이웃 노드들로부터 받은 belief들입니다. 이 두 값을 곱해줍니다.
사이클 그래프
위의 수식은 그래프 내에 사이클 존재를 고려하지 않은 수식입니다.
그래프 내의 사이클에 대한 고려가 왜 필요하냐!
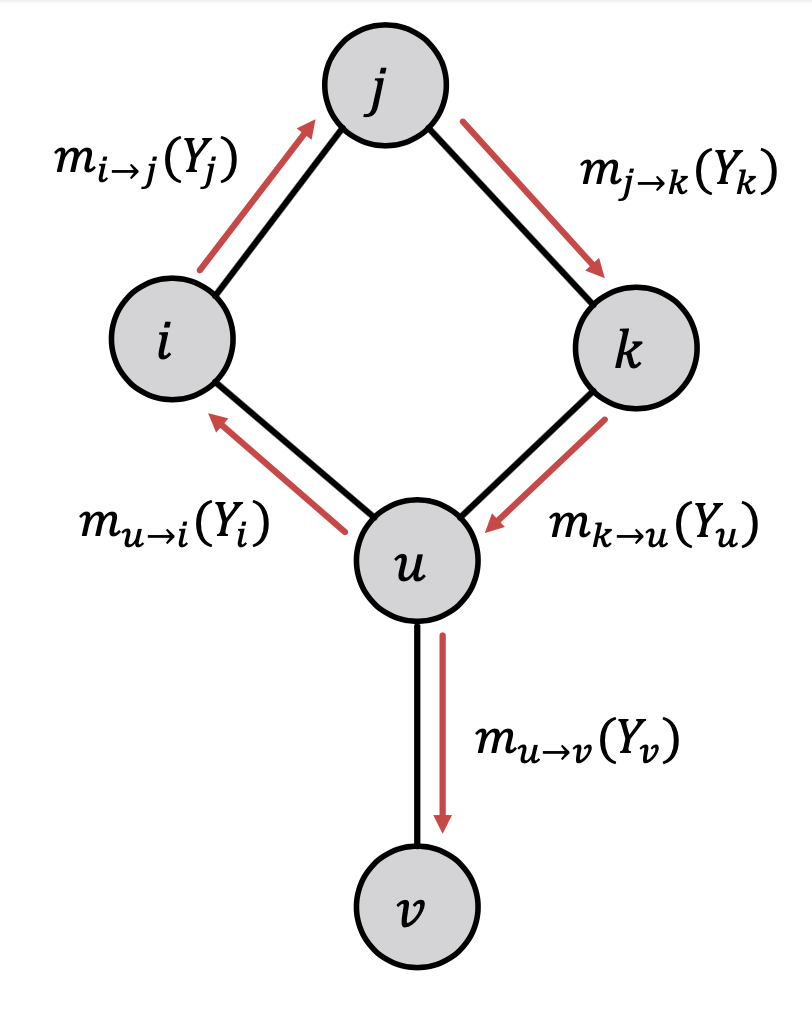
위와 같이 생긴 그래프가 바로 사이클이 있는 그래프인데요.
다음과 같이 계속 belief를 주고 받는다고 합시다. u -> i -> j -> k가 계속해서 반복되겠죠?

예를 들어 T, F 값을 가진 belief가 있다고 가정합시다. 초기에는 T : 2, F : 1값을 받지만 사이클을 돌수록 값이 점점 커질 것입니다.
그렇다면 이 식은 절때로 수렴하지 않겠죠?(계속 커지다보니 발산하게 될 것입니다.)
엄청난 문제같습니다!!!
하지만!
생각보다 사이클은 크게 문제가 되지 않는다고 합니다.
왜냐하면 실제로 우리가 적용하는 그래프들은 위의 그래프보다 훨씬 크고, 그래프 내에 사이클은 큰 부분을 차지하지 않는다고해요!
따라서 위에서 언급한 알고리즘이 잘 작동한다고 합니다.
지금까지 설명했던 Belief Propagation은 구현이 쉽고, 어떤 그래프 모델이더라도 potential matrix를 구성할 수 있기 때문에 적용하기 좋습니다.
하지만! 위에 말씀드렸던것 처럼 수렴하지 않는 상황이 종종있습니다.
'인공지능공부 > 그래프' 카테고리의 다른 글
스탠포드 강의를 듣고 정리한 내용입니다.
지난 포스팅에서는 Relational Classification, Iterative Classification에 대해서 알아보았습니다.
이번 포스팅에서는 Belief Propgation에 대해서 알아보겠습니다.
Belief Propagation
지난 포스팅에서 설명한 방법론들을 살펴보면 모두 이웃 노드로부터 받은 확률의 가중 평균으로 자기 자신을 업데이트합니다. (초기에는 라벨로 부터 받죠) 이 말은 즉, 주변 노드가 현재 노드의 결정에 영향을 준다는 말이죠.

학교에서 쪽지 돌리는 것을 생각해보죠. 서로 가깝거나 연결된 사람에게 쪽지를 돌릴 수 있습니다. 이것을 이웃 노드가 belief를 준다 라고 표현합니다. 노드는 이웃 노드들로부터 belief를 받아 자신을 업데이트하고, 또 다른 주변 노드에게 업데이트된 belief를 전달합니다. 이렇게 계속 전달하다보면 멀리 있는 노드의 belief도 받을 수 있게 됩니다. 받는 것은 바로 이웃에게 받지만, 그 이웃은 또 이웃의 이웃에게 받아온 정보이기 때문이죠!
예시
몇 가지 예를 들어 보겠습니다. 첫 번째로는 일렬로 된 path graph입니다.

위의 그래프에 노드가 몇개인지 노드 간의 iteract(message passing)를 통해 세보도록 하죠! 시작 노드는 1입니다.

위와 같이 count용 변수를 m이라고 할 때, 각 노드는 받은 메세지에 1을 더하여 다음 노드로 넘겨줍니다. 이렇게 하면 마지막 노드에서 노드의 최종 개수를 알 수 있죠.
두 번째 예시는 트리 형태의 그래프입니다.

위의 그래프에서도 같은 목표를 가지고 있고, leaf 노드에서 root노드로 가면서 노드를 카운트 합니다.
각 노드는 자신의 leaf node로부터 받은 값을 모두 더하고, 자기 자신인 1을 더하여 다음 노드에게 전달해줍니다.

root노드까지 반복하면 위와 같이 노드 개수를 구할 수 있습니다.
전에도 언급했지만, 위의 예를 통해 다음 노드로 전달하는 것은 이전 노드로부터 받은 값이고, 노드가 어떤 값을 받았냐에 따라 전달하는 값은 변한다는 것을 알 수 있습니다.
지금까지는 각 노드들이 정보를 어떻게 전달하는지 간단한 예시로 확인해 보았습니다.
이제부터는 실제 알고리즘이 어떻게 되어있는지, 어떤 정보를 전달하는지 알아보겠습니다.
작동 과정
실제 어떻게 작동하는지 알기 전, 몇 가지 개념들을 정의하겠습니다.
- ψ : ψ(Yi, Yj)는 이웃 노드 i의 라벨이 Yi일 때, 노드 j가 Yj일 확률의 비중으로, 각 노드가 이웃 노드의 클래스에 대한 영향력을 행렬로 표현한 것
- ϕ : ϕ(Yi)는 노드 i가 라벨 Yi일 확률
- mi→j(Yj) : 노드 i의 메세지가 노드 j로 전달 되는 것
- L : 모든 라벨을 포함하는 집합

다음과 같은 그래프가 있다고 가정합시다.
현재 그래프의 목적은 기준 노드 i에서 부터 목적 노드 j까지 belief를 보내는 것입니다.
이를 위해서는 아래와 같은 과정들을 거칩니다.
1. 초기 모든 메세지는 1로 초기화
2. 노드 간의 메세지 전달을 계속 반복(아래 수식 참고)

왼쪽 부터 오른쪽으로 수식을 설명하겠습니다.
분홍색
모든 종류의 라벨에 대해 현재 노드 i의 가능성을 측정
초록색
i노드의 각 라벨 마다 j노드가 Yj라벨을 가질 확률을 계산(쉽게 말하면 노드 i의 라벨에 따른 노드 j의 라벨 분포? 라고 생각하시면 될것같습니다. 왜냐하면 노드 j도 결국 이웃 노드인 노드 i의 영향을 받기 때문이죠.)
빨간색
i가 어떤 라벨을 가질지 확률을 계산해 줍니다.
파란색
기준 되는 노드(i)로 오는 모든 belief들을 모아줍니다.(노드 i가 Yi라벨일 belief를 넘겨받음)
빨간색
i가 어떤 라벨을 가질지 확률을 계산해 줍니다.
위의 수식을 반복하여 수렴한다면 아래와 같이 실제 확률이 계산됩니다.
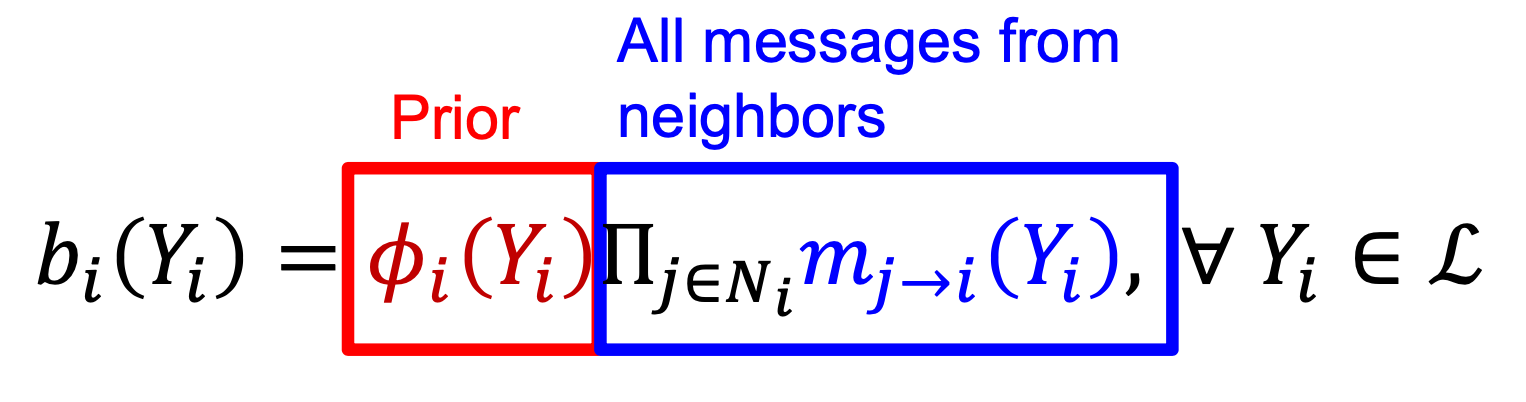
빨간색
노드 i가 라벨 Yi를 가질 확률
파란색
노드 i가 이웃 이웃 노드로부터 오는 모든 belief의 모음
수식을 설명해 보자면, bi(Yi)는 노드 i가 Yi일 확률과 노드 i의 이웃 노드들로부터 받은 belief들입니다. 이 두 값을 곱해줍니다.
사이클 그래프
위의 수식은 그래프 내에 사이클 존재를 고려하지 않은 수식입니다.
그래프 내의 사이클에 대한 고려가 왜 필요하냐!

위와 같이 생긴 그래프가 바로 사이클이 있는 그래프인데요.
다음과 같이 계속 belief를 주고 받는다고 합시다. u -> i -> j -> k가 계속해서 반복되겠죠?

예를 들어 T, F 값을 가진 belief가 있다고 가정합시다. 초기에는 T : 2, F : 1값을 받지만 사이클을 돌수록 값이 점점 커질 것입니다.
그렇다면 이 식은 절때로 수렴하지 않겠죠?(계속 커지다보니 발산하게 될 것입니다.)
엄청난 문제같습니다!!!
하지만!
생각보다 사이클은 크게 문제가 되지 않는다고 합니다.
왜냐하면 실제로 우리가 적용하는 그래프들은 위의 그래프보다 훨씬 크고, 그래프 내에 사이클은 큰 부분을 차지하지 않는다고해요!
따라서 위에서 언급한 알고리즘이 잘 작동한다고 합니다.
지금까지 설명했던 Belief Propagation은 구현이 쉽고, 어떤 그래프 모델이더라도 potential matrix를 구성할 수 있기 때문에 적용하기 좋습니다.
하지만! 위에 말씀드렸던것 처럼 수렴하지 않는 상황이 종종있습니다.
