등장 배경
Word2vec, Fasttext와 같이 개별 단어에 대해 의미있는 표현들을 학습하는 word embedding 기법들은 많은 발전을 이루었는데요.
여러 단어 혹은 구가 나열된 문장의 표현을 학습하는 sentence embedding 기법들은 word embedding에 비해 많이 부족합니다.
sentence embedding은 크게 두 가지로 나누어질 수 있는데요.
첫 번째는 unsupervised learning을 통해 universal sentence representation을 만드는 방법입니다.
대표적인 예로는 Skip Tought vector, ParagraphVector 등이 있습니다.
※ universal sentence representation이 뭐죠?
문장의 의미를 잘 표현하는 벡터 표현을 생성하는 모델입니다. 줄여서 USR이라고도 합니다.
두 번째는 특정 task를 위해 학습하는 방법인데요.
이 방법은 supervised learning을 통해 학습하고, downstream task와 합쳐서 사용됩니다. word embedding 이후에 CNN, RNN등의 모델을 거쳐 sentence representation을 얻고, task specific하게 사용할 수 있습니다.
이 방법에 attention mechanism을 적용할 수도 있는데요. 일반적으로 attention이라고 하면 서로의 비교 대상이 있어야 하기 때문에 적용하기가 어렵죠. (적어도 두 개 이상의 문장이 있어야 서로 attention을 계산할 수 있기 때문입니다.) 따라서 대부분의 네트워크에서는 attention의 적용이 어려웠습니다.
하지만! 이 모델은 두 개 이상의 문장을 사용하지 않고도 attention을 이용할 수 있는 방법을 제안했습니다.
바로 self-attention을 이용하는 방법입니다. (논문은 여기 있습니다)
지금은 Transformer, Bert, GPT 등의 유명한 모델들이 많이 제안되어서 self-attention이 너무 당연한것처럼 들리실수 있는데요. 이때까지만 해도 아주아주 신선한 방법이었습니다!
학습 과정

전체적인 작동 과정은 위의 (a)와 같습니다.
학습 과정은 크게 3가지로, 첫 번째는 입력된 문장으로 attention score를 구하는 부분, 두 번째는 attention score로 최종 출력 벡터를 구하는 부분, 마지막으로 loss를 구하는 부분 으로 나눌 수 있을 것 같습니다. (제가 나눈 기준입니다..!)
입력 문장으로 attention score 구하기
1. 입력 초기 임베딩
먼저 입력이 어떻게 생겼는지 한번 볼까요?
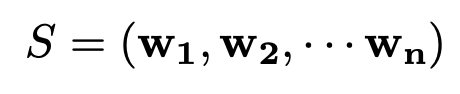
입력은 S로 정의할건데, S는 하나의 문장을 뜻합니다. 그 문장은 n개의 단어 벡터 W로 구성되어있죠.
여기서 w는 d 차원을 가집니다. 즉 S문장은 [n, d]차원을 가지는 하나의 벡터입니다.
예를 들자면 "나는 오늘 너무 행복해"라는 문장이 있다고 합시다. 이 문장의 각 단어를 300차원을 가지는 word2vec으로 초기 임베딩을 한다면, "나는", "오늘", "너무", "행복해" 라는 4개의 단어가 나올 것이고, 각 단어는 300차원을 가질 것입니다. 따라서 [4, 300]이 되는 것이죠!
2. 문맥 정보 임베딩

이렇게 초기 임베딩된 문장은 "단어"위주로 임베딩 되었기 때문에, 문맥간의 임베딩을 잘 할수 있도록 LSTM에 태워줍니다. 이 때, bi-LSTM을 사용합니다.
여기서 LSTM 결과로 나오는 벡터를 u차원이라고 하면, bi-LSTM기 때문에 2u차원이 됩니다. 따라서 [n, 2u]차원 벡터를 얻을 수 있습니다.
이 결과로 나온 벡터는 아래와 같이 표현할 수 있습니다.

위의 h들은 각 단어의 bi-LSTM결과라고 생각해 주시면 됩니다. 각 h들은 2u차원을 가집니다.
3. attention score구하기

문장을 고정된 크기로 임베딩하기 위해서 위의 H벡터를 linear combination을 통해 일정한 크기로 만들어줍니다. 여기서 Ws1, Ws2를 이용하는데요. 그냥 간단하게 '두 계층의 fc를 통해 attention matrix를 구한다.' 라고 생각하시면 됩니다.
- Ws1은 [da, 2u]크기를 가지며, HT인 [2u,n]과의 결합을 통해 [da, n]이 됩니다.
- Ws2는 [1, da]의 크기를 가지며, 위의 벡터와 곱해질 때, [1, n]차원이 됩니다.
마지막으로 이 차원에 softmax를 취해줌으로써, 각 요소들의 합이 1이 되게합니다.
여기서 나온 [1, n]이 의미하는 것은 각 단어 n개의 중요도입니다. 즉, 어느 단어가 중요한지에 대해 0~1사이의 값으로 각각 나타낸 것이죠.
이것을 attention score라고 합니다.
여기서 잠깐!
위의 벡터는 [1, n]차원을 가지죠? 한 개의 시각으로 문장의 각 단어를 본것입니다.
즉, 문장에서 중요한 부분이 한 부분만 있다고 가정하게 되는데요. 예를 들어 "고양이와 강아지"라는 문장에서 "고양이", "강아지"가 모두 중요할 수 있습니다. 따라서 Ws2의 1을 r로 바꿔줍니다. 즉, Ws2는 [r, da]차원을 가지며, 'r개의 시각으로 문장을 바라본다'라고 보시면 될것같습니다.
attention score로 최종 출력 벡터 구하기
1. attended vector 구하기


위에서 attention score를 구했죠? 이것을 초기 임베딩된 벡터에 곱해주기만 하면 됩니다! matrix로 표현하면 A라고 할 수 있죠. 이것을 곱해주면 attended vector M을 구할 수 있습니다. A는 [r, n], H는 [n, d]를 가지기 때문에, 최종 벡터 M은 [r, d]가 됩니다.
2. target에 맞게 최종 벡터 추출
여기는 따로 논문에 나와있지는 않은데요. 위에서 나온 벡터 M을 하나의 fc를 거쳐 최종 예측 하시면 됩니다. fc는 [r*d, target]차원을 가질것이며, M을 flatten시켜주고, fc를 거쳐주시면 됩니다!
loss를 구하기
위에서 'Ws2의 [1, da]를 [r, da]로 바꾸면 r개의 시각으로 문장을 바라보는 것이다'라고 말씀드렸는데요.
여기서 "근데 그 시각이 다 비슷하면 어쩌지?"라는 의문이 드실 수 있습니다. 서로 다르게 바라보라고 추가한 부분인데, 다 같은 관점으로 바라본다면 의미없는 반복만 있을 뿐이니, 이부분에 대한 고려도 해야겠죠.
예를 들어 "고양이와 강아지"에서 중요한 부분을 모두 찾으라고 했더니 r개의 관점 모두 "고양이"만 중요한데? 라고 말하는 것과 같습니다
이 모델에서는 실제로 이런 부분에 대한 고려도 했습니다!
바로 일종의 패널티를 주는 방법인데요. Frobenius Norm을 이용합니다.

여기서 ||·||F은 Frobenius Norm을 뜻합니다. 이것은 L2 regularzation term과 비슷한 역할을 하는데요. coefficient를 곱한 뒤에 loss와 더해져 최소화를 시켜줍니다. 위의 I는 단위행렬로 대각 행렬이 1인 행렬을 뜻합니다. 자기 자신을 제외해주기 위해서 대각 요소들을 모두 제거해줍니다.
※ Frobenius Norm 이 뭐죠?
norm이라고 하면 일반적으로 벡터의 크기를 나타내는 양인데요. Frobernius norm은 행렬의 크기를 구하는 경우 사용합니다.

수식을 한번 분석해 보겠습니다. 여기서 A벡터의 각 성분을 a라고 합시다.

A는 최종 단계에서 softmax를 취해줬었죠. 따라서 무조건 0~1사이의 값을 가집니다. 그렇다면 A*AT의 모든 비대각 원소에 대해 각 원소의 곱은 위의 분포를 가지고 있습니다. 여기서 aki는 A의 k번째 요소 벡터를 뜻합니다.

이해하기 쉽게 행렬을 그려봤습니다. A의 자기 자신과의 곱이 모두 0~1사이가 되는게 이해되시나요?!
자 이제 몇 가지 예를 통해서 위의 P를 조금 더 이해해볼까요?
극과 극의 (행렬 A,B)예를 들어볼겁니다. 여기서 r은 3으로 가정합니다.
1. A의 행렬이 모두 같은 단어를 중요하다고 판단한경우

A는 첫 번째 단어만 중요하다고 판단하였습니다. 따라서 모든 관점들이 첫 번째 단어를 1로 아주 강하게 중요하다고 주장중입니다!

이제 트랜스포즈한 행렬과 곱해주면, 모든 요소가 1인 행렬이 나오게 됩니다.
2. B의 행렬이 모두 다른 단어를 중요하다고 판단한경우

각 관점마다 모두 다른 단어가 중요하다고 주장하겠죠!

위에서 나온 값들에서 모두 비대각 원소들의 원소 곱 분포를 구해봅시다.

모두 같은 것을 예상했던 A행렬의 경우 k값에 상관없이 모두 1이 되고, 모두 다르다고 예상했던 B행렬의 경우 k값에 상관 없이 모두 0이 됩니다.
이 결과로부터 같은 단어에 대한 attention weight가 관점마다 다를수록 더 낮은 값을 가지고, 같을 수록 더 높은 값을 가집니다.
즉, 더 다양한 관점으로 볼수록 loss가 줄어들게 됩니다!
'인공지능공부 > 자연어처리' 카테고리의 다른 글
| Self-Attentive Sentence Embedding(SASE) 구현해보기 (0) | 2023.03.22 |
|---|---|
| fasttext의 모든 것 (0) | 2023.03.20 |
| word2vec의 모든 것 (0) | 2023.03.18 |
| [huggingface🤗] 3.Trainer사용해보기 (0) | 2023.03.14 |
| [huggingface🤗] 2.Auto Class사용해보기 (2) | 2023.03.13 |
