스탠포드 강의를 듣고 정리한 내용입니다.
지난 포스팅에서는 GNN이 어떻게 사용되는지 설명하기 전 GNN Framework에 대해 간단하게 정리했습니다.
이번 포스팅에서는 단일 레이어에서 GNN이 어떻게 동작하는지 살펴보겠습니다.
GNN Layer

GNN의 레이어는 Message, Aggregation 이렇게 두 단계로 나뉠 수 있습니다.
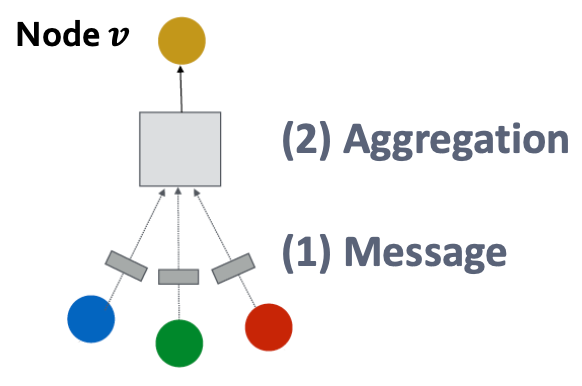
레이어의 목표는 현재 기준이 되는 노드의 주변 노드를 입력받아 각 메세지들을 계산하고, 압축하여 현재 노드를 갱신하는 것 입니다.

조금 더 자세히 보시면 다음과 같습니다. 기존에 자기 자신의 노드와 주변 노드를 입력받아 메세지를 결합하여 노드를 업데이트합니다.
그럼 이제 각 단계를 살펴볼까요?
1. Message Computation

메세지 계산단계는 이전 레이어에서 온 정보들을 정해진 메세지 함수인 MSG를 통과하여 이번 레이어의 정보로 만드는 과정입니다.

수식은 위와 같습니다. 이전 단계의 노드들을 '각각' 입력받고, 각 노드의 결과를 얻습니다. matrix 계산으로 한번에 계산은 되겠지만, 아직 합쳐지지 않은 상태입니다. 따라서 n개의 노드는 n개의 새로운 메세지를 얻습니다.
matrix 계산으로 나타내면 아래와 같은 수식을 얻을 수 있겠네요.

2. Aggregation

aggrgation은 말 그대로 MSG함수에 의해 변환된 각 노드들을 AGG함수로 모으는 역할을 합니다.

일반적으로 위와 같이 수식을 만들 수 있습니다. 여기서 AGG함수라고 하면 Sum, MeaN, MaX 등을 생각할 수 있습니다.
예를 들어서 Sum을 사용한다고 하면, 아래와 같이 수식을 나타낼 수 있습니다.

Issue
위에서는 GNN의 레이어가 어떻게 작동하는지 간단하게 이야기했는데요. 여기서 문제점이 하나 있습니다. 바로 노드 자체 정보가 손실될 수 있다는 것인데요. 바로 직전 단계의 노드 정보가 Aggregation 단계에서 다른 노드들이랑 함께 합쳐져버리기 때문에, 어떤 정보가 과거 자신의 정보인지 구별할 수 없게된다는 것입니다.
그렇다면 어떻게 해결해야할까요?!
여기서는 두 가지 관점으로 해결책을 제시하고 있습니다.
1. Message
메세지 관점에서는 기준 노드의 직전 상태와 이웃 노드들의 MSG함수를 따로 놓는 것입니다.
먼저 기존 식을 한번 살펴보면,

이렇게 과거 기준 노드, 이웃 노드를 구분하지 않고 무조건 w를 곱해주었습니다.
하지만 이를 조금 변형한다면,

다음과 같이 기준 노드를 분리함으로써 기준 노드를 구분할 수 있습니다.
2. Aggregation
집계의 관점에서는 이웃 노드만 집계하고, 기준 노드의 직전 상태는 concat하는 것입니다.

기존에는 위와 같이 모든 노드들을 AGG함수로 압축시켜주었습니다.
하지만 이를 조금 변형하면,
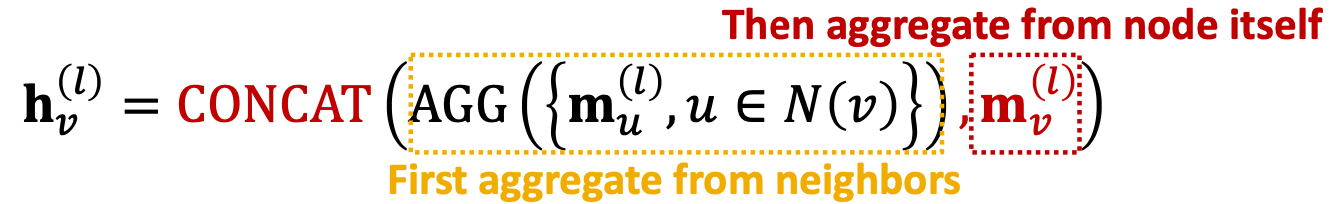
기준 노드들만 압축시켜준 뒤, message과정을 통해 얻은 기준 노드의 과거를 concat시켜줍니다. (단순히 뒤에 붙여준다는 의미입니다.) 이렇게 되면 과거 기준 노드는 압축되지 않기 때문에, 자기 자신의 정보를 살려서 업데이트를 할 수 있게 됩니다.
따라서 위의 두 개선점을 적용시키면, 일반적인 GCN layer는 다음과 같이 구성됩니다.

여기에 하나 추가적으로 Nonlinearity(activation)을 거쳐줍니다!(sigmoid, relu, softmax 등등을 뜻합니다. )
자 그럼 이제 실제 모델에서 어떻게 사용되는지 알아봅시다!
GCN(Graph Convolutional Neural Network), GraphSAGE, GAT(Graph Attention Network) 등을 살펴봅시다.
1. GCN
먼저 GCN의 한 레이어를 볼까요?
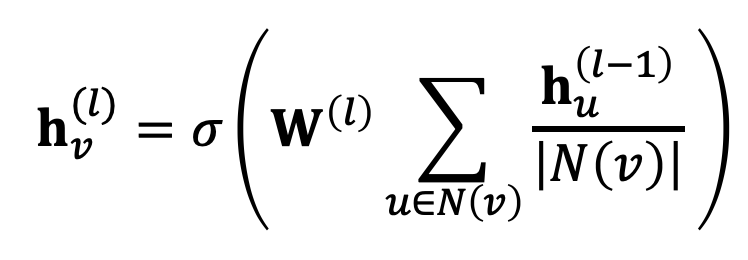
이 수식에서 Message, Aggragation을 찾아보겠습니다.

조금 더 자세히 풀어서 써보겠습니다.
1. Message

GCN에서는 노드 degree로 normalize를 해주기 때문에 결과를 각 N(v)로 나누어줍니다.
2. Aggregation

여기서는 단순히 Sum을 통해 message를 통과한 노드들을 집계해주고, activation 함수를 거칩니다.
GCN에서는 위에서 설명한 Issue가 개선되지 않은 상태입니다!
2. GraphSAGE
GraphSAGE의 레이어를 살펴보죠!

GCN에 비해 수식이 굉장히 길어졌죠?
Message 부분은 큰 차이가 없기 때문에 AGG 함수 내에서 수행이 된다고 가정합니다.
Aggregation
여기서 Aggregation은 총 두 단계로 이루어집니다. 살짝~ 먼저 말씀드리면 Issue때 개선했던 부분입니다.
1. 먼저 이웃 노드들에 대한 집계를 수행합니다.

2. 이후 과거 기준 노드와 Concat시켜줍니다.

그럼 AGG는 어떤 것이 쓰일까요?
여기서는 Mean, Pool, LSTM 총 3개를 이야기합니다.
(1) Mean
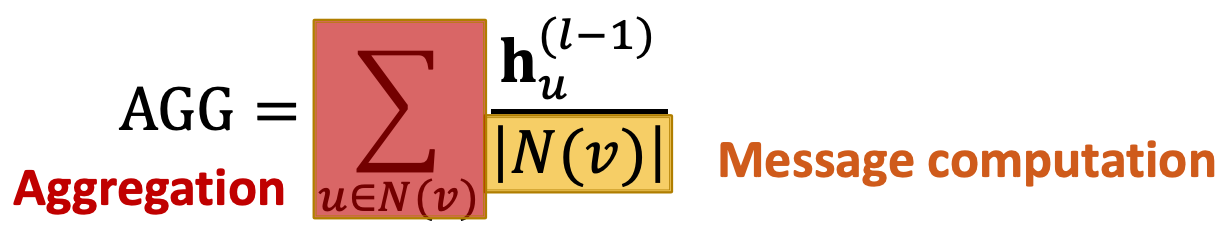
이는 GCN에서 보았던 부분과 유사하죠? 단순히 평균을 구해주는 과정이며, message computation 과정 자체가 GCN에서 처럼 normlization 역할을 합니다.
(2) Pool

Pooling이라고 생각해 주시면 되는데요. 각 노드들을 어떤 파라미터 W에 곱해준 뒤, 평균을 취해주는 방법입니다.
(3) LSTM

LSTM은 sequence데이터를 주로 넣는데, 여기서 노드를 넣게되면 순서를 학습할 수 있습니다. 따라서 노드를 계속 섞어가며 학습시켜주셔야 이러한 부분이 약하게 학습됩니다.
L2 Normalization
GraphSAGE는 모든 레이어에서 L2 정규화를 시켜줍니다. 따라서 모든 레이어의 output은 norm이 1이 됩니다. 이러한 방법은 성능 자체를 향상시킬 수 있다고 합니다.
3. GAT
GAT는 앞의 방법들과 조금 다른 특징을 가지고 있습니다. 바로 attention이 추가되었는데요.
한번 이해해봅시다!

GAT의 수식은 위와 같습니다. 기존에는 보지 못했던 α인자가 등장했네요!
사실 GCN, GraphSAGE 에도 이와 비슷한 역할을 하는 부분이 존재는 하지만, 아래와 같이 모두 동등하게 정보를 받고있었습니다.

하지만 GAT에서는 "동등하게 받지 말고, 중요한 곳의 정보를 더 많이 받자!"가 목적이기 때문에, attention wieght를 이용합니다.
그럼 어떻게 attention이 적용되는지 조금더 구체적으로 살펴볼까요?
evu
evu은 기준 노드 v에게 이웃 노드 u가 얼마나 중요한지를 나타냅니다.

이는 a라는 어떠한 방법에 의해서 노드 u, v간의 유사도를 계산합니다. 단순히 기준 노드와 이웃 노드 하나를 계산하기 때문에 절대 중요도를 의미한다고 볼 수 있습니다.
αvu
αvu은 마지막 attention weight를 뜻하고, 이는 softmax함수에의해 합이 1이됩니다.
즉, 위에서 계산된 evu를 softmax취해준다고 생각하시면 됩니다.

이는 기준 노드의 하나의 이웃이 아닌 모든 이웃들을 고려하기 때문에 상대 중요도를 의미한다고 볼 수 있습니다.
따라서 다음과 같이 각 레이어의 노드 값을 구할 수 있습니다.


여기서 우리가 정의하지 않은 한 가지가 있는데요.
바로 절대적인 중요도를 구하는 함수인 a입니다.
이 함수도 GraphSAGE의 aggregation함수처럼 여러가지가 있는데요. 몇가지만 소개해보겠습니다.
1. 단순 concat
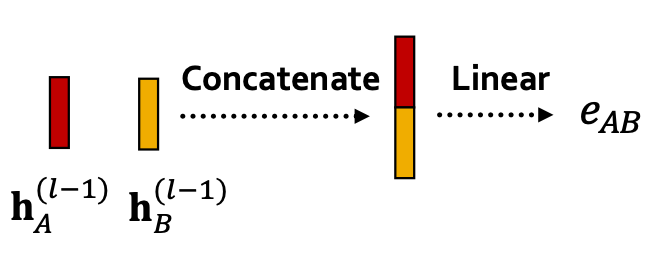
먼저 위와 같이 두 노드 벡터를 단순히 concat해주고 fc 레이어를 통과시켜주는 방법입니다.

정말 간단한 방법이긴 하지만 두 노드의 유사성을 찾기에 적당한 방법인것 같지는 않습니다.
2. Multi-head attention
말 그대로 여러개의 attention을 진행하는데요.

노드를 업데이트할 경우 각각 다르게 초기화된 α를 이용합니다.
이후 노드의 결과를 concat하거나 sum시켜주고 최종 값을 구합니다.

마지막으로 attention을 사용하는 것이 어떤 장점이 있는지 살펴봅시다!
여기서는 총 4가지를 언급하고 있습니다.
computationally efficient
attention 연산은 그래프의 모든 엣지들이 병럴로 계산될 수 있습니다. 따라서 매우 빠르게 학습이 가능합니다.
storage efficient
그래프를 sparse matrix로 저장할 수 있기 때문에 메모리 측면에서 효율적이라고 할 수 있습니다.
localized
attention은 주변 노드에 대해 어디에 집중해야하는지 잘알려줍니다. 즉, local적인 특징을 잘 알 수 있습니다.
inductive capability
edge-wise이기 때문에, global graph structure에 크게 영향을 받지 않습니다.
GNN Layer in Practice
GNN의 각 레이어도 다른 딥러닝 모델처럼 아래와 같은 기법들을 적용시킬 수 있습니다.

Batch Normalization
batch normalization은 학습을 안정적으로 하는 것을 목적으로 하죠.
각 노드 임베딩을 batch 단위로 입력받을 때, 그 배치 단위를 정규화 시켜주는 것을 뜻하죠.

Dropout
오버피팅을 방지하기 위해 사용하는 방법으로, 각 fc 레이어에 몇몇 뉴런들을 off시켜줍니다.

GNN에서는 아래와 같이 사용합니다.

위의 수식들을 보면 message에서 fc 변환이 많이 일어났죠? 이 부분에서 dropout을 이용합니다.
