스탠포드 강의를 듣고 정리한 내용입니다.
앞의 포스팅에서도 언급했지만, 그래프는 크게 3가지의 작업을 할 수 있습니다.

오늘은 위의 방법들 중 Nodel-level에 대해서 포스팅하도록 하겠습니다.
Node-level 작업들

Node-level 작업은 네트워크가 주어지고, 각 노드들이 위와 같이 2개의 라벨을 가진다고 했을 때, 라벨이 달리지 않은 노드에 대해 어느 라벨을 가질지 예측하는 작업을 뜻합니다. 왼쪽에 있는 회색 노드들은 라벨이 붙어있지 않은 노드들인데, 이것을 ML로 학습시켜 라벨을 가지도록합니다. 마치 semi-supervised 학습처럼 보이죠.
위의 작업을 가능하게하는 node feature extraction에 대해서 알아보도록 하겠습니다.
- Node degree
- Node centrality
- Clustering coefficient
- Graphlets
Node Degree
degree라는 것은 이전 포스팅에서도 언급했듯이 노드에 연결되어있는 엣지의 수를 뜻합니다. Node Degree방법은 말 그대로 노드를 연결된 엣지의 수로 표현한다는 것인데요.

위의 예시를 보면 정말 쉽게 이해하실 수 있습니다. 노드 B를 예로 들면, B의 degree는 2이기 때문에 노드 B는 2로 표현됩니다.
이 방법은 정말 간단하지만, 모든 노드와의 관계를 동일하게 생각합니다. 즉, 노드와 연결된 엣지가 '무엇'인지 전혀 신경쓰지 않고 단순 개수만 고려합니다. 따라서 같은 수의 degree를 가지는 노드가 있다면, 구별하기가 어렵습니다. 이런 feature를 ML의 입력으로 넣는다면, 서로 다른 노드지만, degree가 같기 때문에 같은 값을 예측하게 되겠죠.
Node Centrality
node centrality는 노드가 얼마나 중요한지를 고려하는 방법입니다.
노드의 중요성을 이용하여 feature를 만드는 방법도 굉장히 다양한데요. 여기서 몇가지만 알아보도록 하겠습니다.
Engienvector centrality
기준이 되는 노드 v가 중요한 주변 노드에 둘러싸여 있다면, 그 노드 또한 중요한 노드가 됩니다. 페이지 랭크 알고리즘과 굉장히 유사하죠.

Engienvector centrality는 위의 식을 만족합니다.
여기서 우리가 중요도를 구하고자 하는 노드의 벡터는 Cv이고, λ는 정규화 인자입니다. N(v)는 노드들의 집합을 뜻합니다.
해석을 해보자면, 노드 v의 중요도 벡터 Cv는 노드 v의 주변 노드 벡터들의 합을 정규화한 것입니다.
즉, 중요한 사람들이 나랑 관계가 있다면 나도 중요한 사람이다! 라는 것을 뜻합니다.

Engienvector centrality를 구하는 식은 인접행렬 A를 이용하여 위와 같이 나타낼 수도 있습니다. 여기서 c는 각 노드들의 중요도 벡터를 뜻합니다.
Between centrality
이 방법은 노드가 중요한 '커넥터'라면 중요도가 높아집니다. 즉, 어느 두 노드 사이의 최단 거리를 구할 때, 기준이 되는 노드가 항상 포함된다면 중요한 노드라고 가정합니다.

따라서 다음과 같은 식을 만족합니다.
한번 예를 들어서 살펴보도록 하겠습니다.

Cc를 예로 들어 보겠습니다.
- s = A, t = B
- A에서 B까지 가는 최단 경로는 A-C-B 1개가 있고, 이 때 C를 포함하는 방법도 1개입니다. 따라서 1입니다.
- s = A, t = D
- A에서 D까지 가는 최단 경로는 A-C-D 1개가 있고, 이 때 C를 포함하는 방법도 1개입니다. 따라서 1입니다.
- s = A, t = E
- A에서 E까지 가는 최단 경로는 A-C-D-E 1개가 있고, 이 때 C를 포함하는 방법도 1개입니다. 따라서 1입니다.
- s = B, t = D
- B에서 D까지 가는 최단 경로는 B-D이며, 이 때 C를 포함하는 방법은 0개입니다. 따라서 0입니다.
- s = B, t = E
- B에서 E까지 가는 최단 경로는 B-D-E이며, 이 때 C를 포함하는 방법은 0개입니다. 따라서 0입니다.
- s = D, t = E
- D에서 E까지 가는 최단 경로는 D-E이며, 이 때 C를 포함하는 방법은 0개입니다. 따라서 0입니다.
Closeness centrality
이 방법은 다른 노드와의 거리가 가까울수록 중요한 노드라고 가정합니다.
실제로 가장 중심에 있는 노드일수록 다른 노드에게 가는 거리가 짧아집니다.

closeness centrality는 위의 식을 만족합니다.
이번에는 예를 통해서 한번 계산해보겠습니다.

CA를 예를 들어볼까요?
- A-B : A에서 B로 가는 최단 거리는 2입니다.
- A-C : A에서 C로 가는 최단 거리는 1입니다.
- A-D : A에서 D로 가는 최단거리는 2입니다.
- A-E : A에서 E로 가는 최단 거리는 3입니다.
따라서 이 모든 거리의 합을 구하면 8이고, 분모 분자를 바꿔주면 1/8이 됩니다.
같은 방법으로 D를 구하면 1/5가 나옵니다. 이는 D가 더 중앙에 있기 때문에 더 큰 값을 가집니다.
Clustering coefficient
clustering coefficient는 기준이 되는 노드와의 연결성 뿐만 아니라 기준이 되는 노드와 연결된 노드간의 연결성을 고려하는 방법입니다.
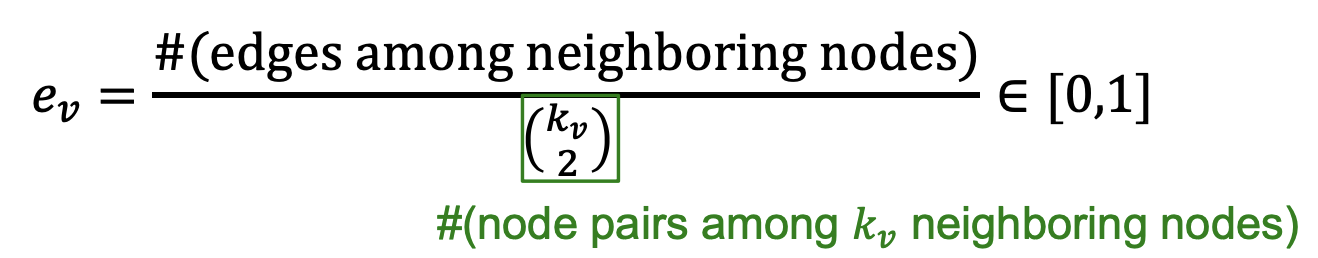
위의 식의 분모는 기준 노드와 연결된 노드들 끼리 연결될 수 있는 모든 엣지의 수이고 분자는 실제로 연결된 엣지의 수입니다.

예를 통해서 한번 이해해보도록 하겠습니다.
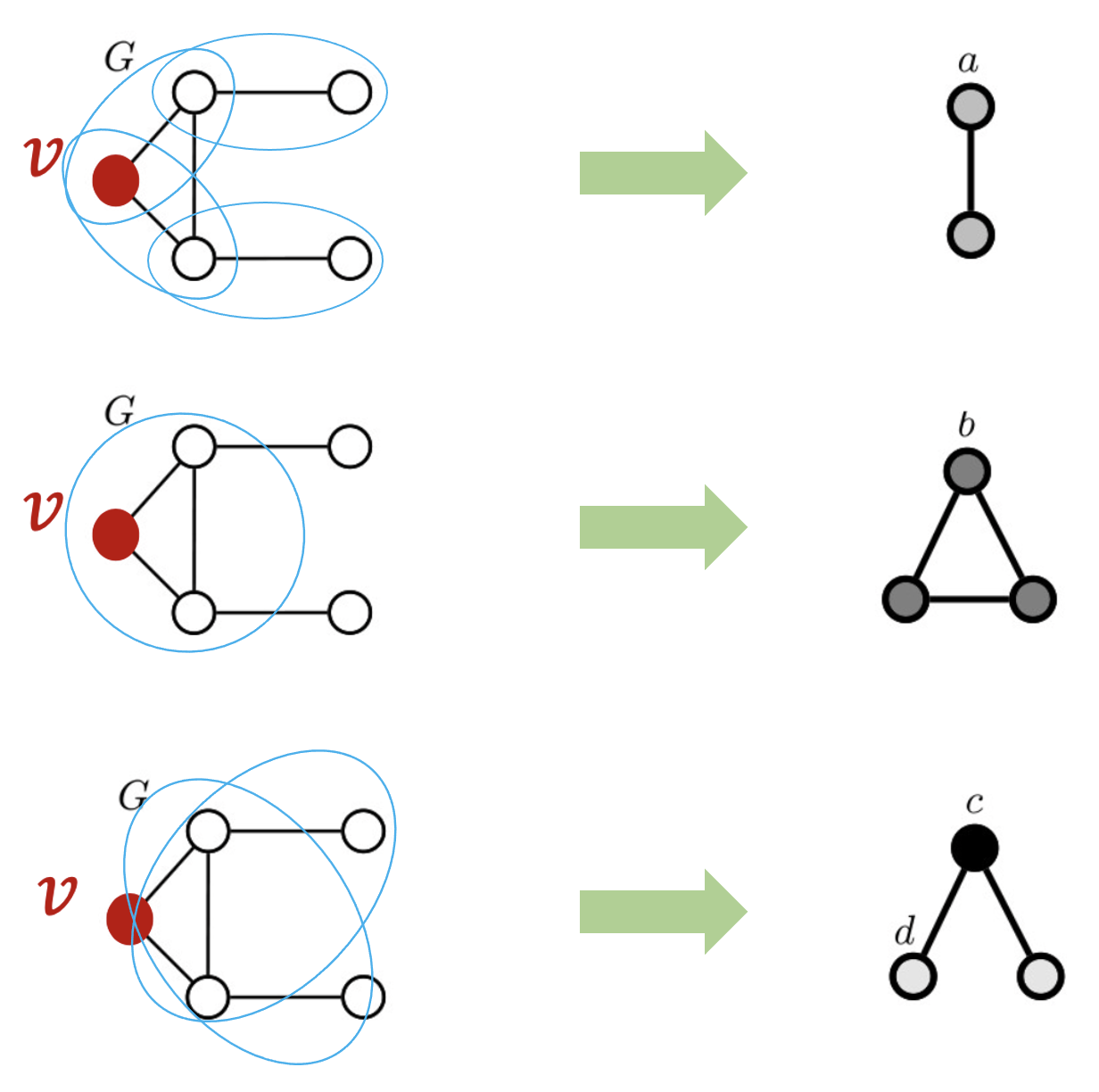
먼저 첫 번째로 가장 왼쪽의 그림을 봅시다.
기준이 되는 노드인 v와 연결된 노드는 총 4개이죠. 4개가 서로 모두 연결될 수 있는 경우의 수는 4C2인 6입니다.
그리고 실제로 빨간색 노드들끼리 6개의 엣지 모두 연결되어있죠. 따라서 6/6이므로 ev는 1이 됩니다.
두 번째로 가운데 그림을 봅시다.
기준이 되는 노드인 v와 연결된 노드는 위와 같죠. 따라서 모두 연결될 수 있는 경우의 수는 6입니다.
실제로 빨간 노드끼리 연결된 엣지는 총 3개입니다. 따라서 3/6이므로 ev는 0.5이 됩니다.
마지막으로 오른쪽 그림을 봅시다.
모두 연결될 수 있는 경우의 수는 6으로 같고, 빨간 노드끼리 연결된 엣지는 없습니다.
따라서 0/6으로 ev는 0이 됩니다.
Graphlets
graphlet은 서로 연결되어있는 sugraph를 뜻합니다. 이때 그래프는 induced, non-isomorphic 을 만족합니다.
- induced subgraph
induced subgraph는 기존 그래프 내에 연결된 모든 엣지들을 포함시키는 subgraph를 뜻합니다.

글로만 읽으면 헷갈릴 수 있으니 그림으로 예를 들어보겠습니다. 위와 같은 그래프가 하나 있다고 가정해봅시다.

초기 그래프에서 위와 같이 두 개의 subgraph를 얻을 수 있습니다. 두 그래프 중 어떤 것이 induced subgraph일까요?
바로 왼쪽입니다. 왜냐하면 실제 그래프에서 (1,2), (1,3), (2,3)이 모두 연결되어있죠? 하지만 오른쪽 subgraph같은 경우 (2,3)이 연결되지 않았지만, 실제 그래프에서는 (2,3)이 연결되어있습니다. 따라서 subgraph라고는 할 수 있겠지만, induced subgraph는 아닙니다.
- non-isomorphic
non-isomorphic개념을 알기 위해서는 먼저 isomorphic개념을 알아야합니다. isomorphic은 두 그래프가 같은 노드 개수를 가지고 있고, 이 두 그래프의 노드들이 똑같이 연결되어있는 것을 뜻합니다.

위의 예시는 그래프의 구성은 다르지만, 노드와 엣지가 모두 같습니다. 따라서 위의 두 그래프는 isomorphic이라고 합니다.
자 이제 그렇다면! 위의 두 조건을 만족하는 그래프란 어떤 그래프일까요?
즉, graphlets이란 무엇일까요?

위의 예를 한번 봅시다. 기존 그래프가 왼쪽 그래프라고 합시다. 왼쪽 그래프를 토대로 graphlets을 3개만 뽑아본다면 오른쪽처럼 뽑을 수 있을 것입니다.
먼저 위의 subgraph들은 induced subgraph를 모두 만족합니다. 또한 전체 그래프에 non-isomorphic하기 때문에 graphlet이다 라고 할 수 있습니다.
graphlet 개념에서 조금 더 나아가 graphlet degree vector를 알아보도록 하겠습니다.
Graphlet Degree Vector(GDV)
graphlet degree vector는 특정 노드를 기준으로 했을 때, 그 노드를 항상 포함하고 있는 graphlet이 몇 개 생길 수 있는지 수치를 이용하는 표현 방법입니다.

위의 예를 다시 한번 가져와보겠습니다. 왼쪽 전체 그래프의 v를 기준으로 GDV를 구해봅시다.
여기서 나올 수 있는 graphlets은 오른쪽과 같다고 했었죠.
1. v노드와 a노드를 매칭 시켰을 경우

v와 a 노드를 매칭 시킬 경우 위와 같이 두 개의 서로 다른 경우를 얻을 수 있습니다.
2. v노드와 b노드를 매칭시켰을 경우

v와 b노드를 매칭 시켰을 경우 서로 다른 모든 경우의 수는 한개 입니다.
3. v노드와 c노드를 매칭시켰을 경우

이 경우에는 v노드를 포함하면 위의 그림과 같이 매칭이 될 수는 있겠죠.
하지만! 우리는 graphlet의 조건을 다시 한번 떠올려볼 필요가 있습니다. 바로 induced subgraph 조건이죠.
실제로는 저 끝 노드 사이에 엣지가 하나 존재합니다. 따라서 v노드와 c노드를 매칭시켰을 경우 서로 다른 모든 경우의 수는 0입니다.
4. v노드와 d노드를 매칭시켰을 경우

v와 d노드를 매칭시켰을 경우 서로 다른 모든 경우의 수는 두개 입니다.
따라서 각각의 subgraph를 a, b, c, d라고 한다면, v노드의 GDV는 [2,1,0,2]입니다.
'인공지능공부 > 그래프' 카테고리의 다른 글
| [Stanford/CS224W] 2. tradition-ml(3) : 전통적인 그래프 레벨 피쳐와 그래프 커널 (0) | 2023.03.02 |
|---|---|
| [Stanford/CS224W] 2. tradition-ml(2) : 전통적인 링크 레벨 작업과 피쳐 (0) | 2023.02.28 |
| [Stanford/CS224W] 1. intro(3) : 그래프 표현의 선택 (0) | 2023.02.25 |
| [Stanford/CS224W] 1. intro(2) : 그래프 ML의 응용 (1) | 2023.02.24 |
| [Stanford/CS224W] 1. intro(1) : 그래프가 필요한 이유 (1) | 2023.02.23 |
