스탠포드 강의를 듣고 정리한 내용입니다.
지난 포스팅에서는 노드 레벨의 작업과 피쳐에 대해서 알아봤습니다.
이번 포스팅에서는 링크 레벨의 작업과 피쳐에 대해서 알아보겠습니다.
Link-level 작업들
Link-level 작업은 두 노드 사이의 관계가 있는지 없는지 예측하는 작업입니다.
보시는 것처럼 노드들의 관계를 랭크로 나타내고 top-K개의 노드 쌍을 예측합니다.
여기에는 크게 2가지 작업이 있는데요.
첫 번째는 기존 그래프에서 랜덤하게 link를 지우고 그 부분을 예측하는 방법이며,
두 번째는 시간에 따라 지나는 관계성을 예측하는 것입니다.
이를 어떻게 적용해야 할까요?
일반적으로는 아래와 같은 프로세스로 작동합니다.
1. 각 노드 쌍(x, y)에 대한 스코어를 계산한다.
- c(x, y)는 x와 y노드의 스코어이다.
2. c(x, y)를 내림차순으로 정렬한다.
3. top-n개의 새로운 링크를 예측한다.
4. 실제로 링크들이 있는지 확인한다.
여기서 가장 중요한것은 바로 c(x, y)! 즉, link feature인데요.
link feature를 만드는 방법에 대해서 알아보겠습니다.
- Distance-based feature
- Local neighborhood overlap
- Global neighborhood overlap
Distance-based feature
distance-based feature는 정말로 간단합니다.
두 노드 사이의 최단 경로가 feature가 되는데요.

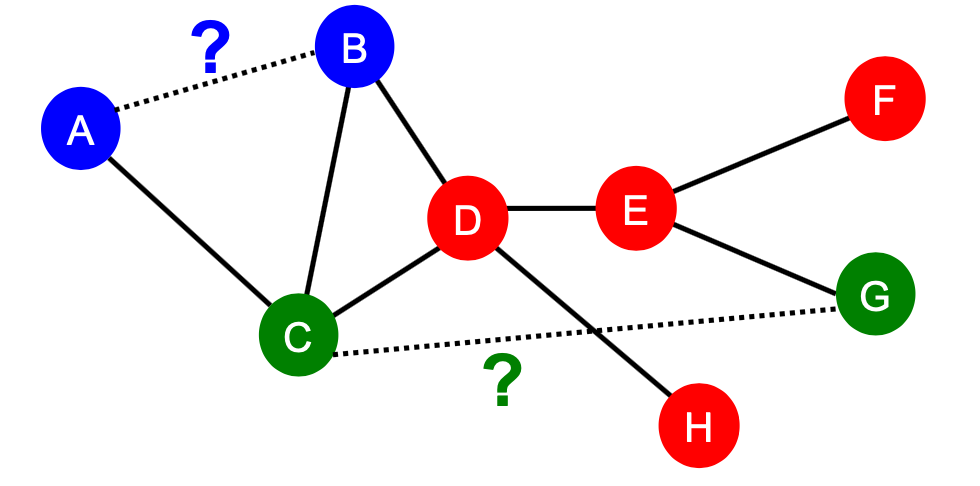
예를 들면 위의 그래프에서 BH의 feature를 구하면 B와 H 사이의 최단 거리는 2가 됩니다. 이는 BE 또는 AB와 같은 값을 가지게 되죠.
여기서 혹시 문제점을 느끼셨나요?
바로 같은 거리에 있는 노드의 링크를 모두 같은 feature로 여기죠. 즉, 이웃 노드들을 무시합니다.
같은 2의 값을 가진다고 하더라도 B와 H사이에는 공통 이웃 노드인 C, D가 있고, B와 E사이에는 공통 이웃이 하나가 있습니다.
B와 H가 공통 이웃이 더 많으니 더 가까운 관계라고 할 수 있겠죠. 하지만 distance-based feature에는 이러한 정보가 담기지 못합니다.
Local neighborhood overlap
이 방법은 말 그대로 이웃이 얼마나 오버랩되는지 체크하는 방법입니다.

예를 들어 위의 그래프에서 B와 F사이의 이웃 노드들이 얼마나 오버랩 되는지 체크하는 방법입니다.
오버랩 되는지 체크하는 방법은 다양하지만 그 중 3가지만 소개하겠습니다.
common neighbors

common neighbors는 말 그대로 두 노드 사이의 이웃들이 얼마나 겹쳐있는지 그 수를 세는 방법입니다.
예를 들어 A,B의 common neighbors를 구하면 C노드 1개가 있기 때문에 1이 됩니다.
jaccard's coefficient

주변에 있는 전체 이웃 노드들 중 겹치는 노드가 얼마나 차지하는지 그 비율을 구하는 방법입니다.
common neighbors를 정규화 했다고 할 수 있겠네요.
예를 들어 A, B의 jaccard's coefficient는 합집합이 C, D로 2이고, 교집합은 C로 1입니다. 따라서 1/2인 0.5가 됩니다.
admic-adar index

이 방법은 위의 두 방법들과 약간 다른데요. 두 노드 공통으로 존재하는 이웃 노드의 degree를 이용합니다.
예를 들어 위의 A, B의 공통된 이웃 노드는 C뿐이므로 C의 degree를 구해주고 log를 취한 뒤, 역수를 취해줍니다.
따라서 1/log(4)가 되겠네요.
이 방법은 A, B 사이의 공통되는 이웃들이 더 적은 degree를 가질수록 A, B사이가 연결될 가능성이 더 크다고 여깁니다.
local neighbor overlap 방법은 기존의 distance-base feature의 단점을 보완했지만 한가지 한계점이 있습니다.

직접 연결되지 않은 두 노드에 대해서는 항상 이웃의 교집합이 0이 됩니다.
A, E노드로 예를 들면, 아래와 같은 식을 만족합니다.

A의 이웃 노드는 C, E의 이웃 노드는 D 밖에 없는데, 이 노드의 교집합은 존재하지 않기 때문이죠.
이것이 왜 문제가 되냐!
바로 시간이 지남에 따라 연결될 가능성이 있는 링크들을 애초에 무시하게 됩니다.
따라서 우리는 그래프를 local하게 볼 것이 아니라 조금더 global 하게 볼 필요가 있습니다.
Global neighborhood overlap
global neighborhood overlap은 위의 단점들을 보완했습니다.
여기서는 katz index 라는 개념이 등장하는데요.
katz index는 주어진 노드들 사이의 모든 길이의 길을 세주는 것을 뜻합니다.
엥? 이게 무슨뜻이지? 싶으실텐데 이부분은 뒤에서 자세히 설명드리겠습니다.
우리는 katz index를 이용하기 위해 각 노드간의 경로 길이가 l인 경우의 수를 셀 수 있어야 합니다.
여기서 바로 인접행렬을 사용한다면 아주 쉽게 구할 수 있습니다.
인접행렬을 이용하는 이유를 간단하게 살펴봅시다.
1. 인접 행렬의 성분이 1이면 두 노드는 이웃이라는 것을 뜻합니다.
- 인접행렬 A의 성분 Auv 가 1일 경우, u와 v는 이웃 노드 입니다.
2. Pluv는 노드 u와 v 사이의 길이가 l인 경로 수입니다. 이때, P1uv=A1uv이 성립합니다.
3. P2uv=A2uv는 아래와 같이 성립함을 알 수 있습니다.


4. 따라서 Pl=Al이 성립합니다.
앞서 katz index는 주어진 노드들 사이의 모든 길이의 길을 세준다고 했는데, 이의 수식을 나타내면 아래와 같습니다.

지금까지 설명했던 인접행렬을 위해서 사용하죠?
여기서 discount factor는 거리가 멀면 덜 중요한 것을 반영하기 위해 설정해 놓습니다.
이 수식을 선형 대수 적으로 나타내면 아래와 같이 나타낼 수 있습니다.

'인공지능공부 > 그래프' 카테고리의 다른 글
| [Stanford/CS224W] 3. node embeddings(1) : 노드 임베딩 (0) | 2023.03.05 |
|---|---|
| [Stanford/CS224W] 2. tradition-ml(3) : 전통적인 그래프 레벨 피쳐와 그래프 커널 (0) | 2023.03.02 |
| [Stanford/CS224W] 2. tradition-ml(1) : 전통적인 노드 레벨 작업과 피쳐 (0) | 2023.02.25 |
| [Stanford/CS224W] 1. intro(3) : 그래프 표현의 선택 (0) | 2023.02.25 |
| [Stanford/CS224W] 1. intro(2) : 그래프 ML의 응용 (1) | 2023.02.24 |
