스탠포드 강의를 듣고 정리한 내용입니다.
지난 포스팅에서는 전통적인 그래프 레벨의 피쳐에 대해 알아보았습니다.
이번 포스팅에서는 본격적으로 노드 임베딩이 어떻게 진행되는지 간략하게 알아보도록 하겠습니다.
Graph Representation Learning
앞의 포스팅에 나왔던 전통적인 Representation 같은 경우에는 아래와 같은 과정으로 진행되었는데요.

이 과정에서 매번 다른 목적의 feature를 수작업으로 추출해야하기 때문에, 이 과정이 편리하지는 않았습니다.
실제로 앞의 포스팅을 되돌아보면 '학습'하는 것이 아니라 직접 다 처리를 했었죠.

하지만 이번 포스팅에서는 feature를 수작업으로 추출하는 것이 아닌 representation learning을 통해 학습하고 자동으로 관련된 벡터를 추출하는데 목적을 두고 있습니다.

위에 보시는 예는 노드 임베딩인데요. 그래프 내의 하나의 노드를 d차원의 하나의 벡터로 임베딩 하는 것이 바로 노드 임베딩의 목표입니다.
즉, 간단하게 말하면 "노드를 하나의 임베딩 공간에 맵핑해준다."라고 생각하시면 됩니다.
네트워크 내에 있는 유사한 노드들이 임베딩 공간에서도 유사하게 임베딩이 되게끔 학습이 됩니다. 네트워크 내에서 가까운 노드들이 임베딩 공간에서도 가깝다는 의미이죠!
따라서 노드 분류, 링크 예측, 그래프 분류 등의 아주 많은 다운스트림 태스크에도 활용될 수 있습니다.

이해가 잘 안되실수도 있으니 그림을 하나 보여드리겠습니다.
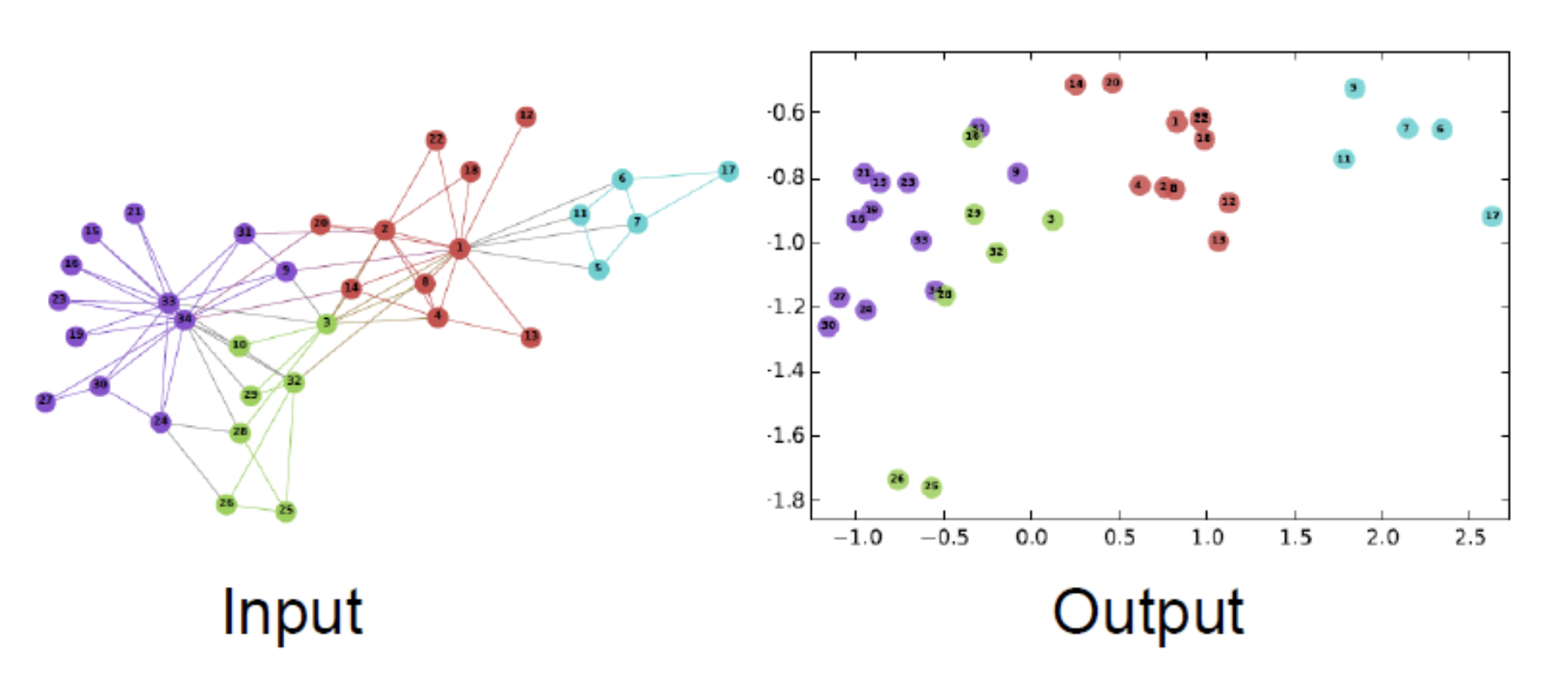
위의 그림은 뒤에서 배울 Random Walk 계열의 DeepWalk 라는 알고리즘의 결과 그림입니다.
보시면 입력으로는 하나의 그래프가 들어가는데, Representation의 결과는 오른쪽과 같이 얻을 수 있습니다.
임베딩 공간에 비슷한 노드가 비슷하게 임베딩 된것이 잘 보이시나요?
같은 색의 노드가 유사한 노드라고 생각하시면, 비슷한 색의 노드가 임베딩 공간에 몰려있는 것을 확인할 수 있습니다.
Node Embedding 과정의 추상적인 정의
그렇다면 노드 임베딩은 어떤 과정을 거칠까요?
이번 장에서는 노드 임베딩의 과정을 추상적으로 한번 정의해보도록 하겠습니다.
왜 추상적인 방법이냐 하면 구체적인 방법론의 이름이 아니라 "추상적으로 이러한 과정을 거쳐서 노드 임베딩이 될것이다." 라는 개념을 정의하기 때문입니다.
배경 정의

본격적으로 노드 임베딩의 과정을 정의하기 전에 몇가지 용어들을 정의하도록 하겠습니다.
위에 그래프가 하나 표현되어 있는데요. 이 그래프는 G입니다.
그래프 내에 있는 도드들은 V, 이들 간의 관계를 하나의 인접 행렬로 표현한 것을 A라고 정의하겠습니다.

이제 우리는 그래프를 가지고 위의 그림과 같은 과정을 거쳐서 노드를 임베딩 스페이스로 매핑을 시켜줄것인데요.
여기서 거치는 이 과정을 인코딩(Encoding, ENC)라고 정의하고, 이와 같은 역할을 하는 것을 인코더(Encoder)라고 하겠습니다.

앞서 말씀드렸다 싶이 우리는 그냥 아무런 수치에 노드를 매핑하는 것이 아니라, "그래프 내에서 유사한 노드들은 임베딩 스페이스 내에서도 유사하게 매핑시킬 것이다." 라고 했습니다. 따라서 representation learning의 목표는 "누 노드가 얼마나 유사하냐"죠.
따라서 임베딩된 노드 벡터들 간의 관계를 기존 그래프의 노드 간의 관계로 어떻게 매핑 시킬지 그 방법을 정의하는 것이 디코딩(Decoding)이라고 하며, 이와 같은 역할을 하는 것을 디코더(Decoder)라고 합니다.
※ 인코더와 디코더
일반적으로 인코더는 입력 값을 특정 벡터로 임베딩 시키는 것을 뜻하고, 디코더는 임베딩 시킨 것을 다시 입력 데이터 형태로 되돌리는 것을 뜻합니다.
예를 들어 자연어 처리에서 "그래프" 라는 단어를 인코더에 넣으면 [0.1233, 0.4324, 5.23123]와 같이 임베딩된 벡터가 출력되고,
이 벡터를 디코더에 넣으면 다시 입력 값의 형태인 "그래프"로 출력됩니다.
여기서도 비슷한 의미를 가집니다.
인코더는 입력 노드 자체를 벡터로 표현하고, 디코더는 벡터 간의 관계를 기존 그래프에서 표현해줍니다.
정리하자면,
- 그래프는 G, 그래프 내에 노드의 집합은 V, 이들의 인접행렬은 A로 표현한다.
- 그래프 내에 노드들을 임베딩 스페이스에 매핑 시키는 것을 인코딩이라 하며, 이는 인코더가 수행한다.
- 임베딩 스페이스에 표현된 representation의 유사도와 기존 그래프 노드 간의 유사도를 비교하는 것을 디코딩이라 하며, 이는 디코더가 수행한다.
입니다.
이제 노드 임베딩이 진행되는 과정을 간단하게 정리해 볼까요?
1. 인코더는 노드를 임베딩으로 맵핑한다.
2. 노드 유사도를 측정할 함수를 정의한다. (보통 내적을 이용하여 유사도를 구합니다.)
3. 디코더는 두 벡터의 유사성을 스코어로 나타낸다.
4. 인코더의 파라미터를 아래의 수식으로 최적화한다. (기존 그래프 내에 노드 유사도가 클수록 벡터 공간 내 임베딩 벡터 유사도도 커져야함)

Encoder
인코더는 위에서 말씀드렸다 싶이 그래프 내에 있는 노드를 임베딩 스페이스에 벡터로 표현하는 것입니다.

다음과 같은데요. 임베딩된 벡터는 z로 표현합니다. 예를 들어 v 노드가 임베딩된 벡터는 zv입니다.
그렇다면 인코딩은 어떻게 진행될까요?
여기서 말하는 가장 간단한 Shallow 방법은 단순히 lookup table을 이용하는 방법입니다.
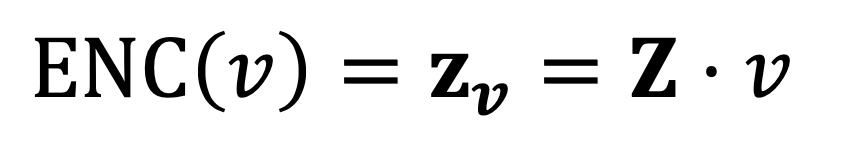
식은 위와 같이 단순 곱으로 정의 될 수 있겠죠.

시각적으로 살펴보자면 결과로는 위와 같은 matrix를 얻을 수 있을 건데요. Z는 모든 임베딩된 노드 벡터의 집합으로 생각하시면 됩니다.
Z벡터의 하나의 컬럼은 하나의 노드 벡터라고 생각하시면 됩니다.
만약 그래프 G에 V가 v1, v2, v3 이렇게 3개 존재하고, lookup table을 이용하여 차원이 10인 벡터로 변화했다고 가정합시다.
최종적으로 Z는 (10,3)행렬이 만들어질 것입니다. 여기서 첫 번째 컬럼은 v1, 두 번째 컬럼은 v2, 세 번째 컬럼은 v3 노드의 벡터를 뜻합니다.
Decoder
디코더는 말 그대로 인코더를 거쳐 표현된 노드 벡터를 다시 원래 데이터로 데려가서 어떻게 표현해줄지 고민을 합니다.
즉, "기존 그래프에서 가까운 두 노드는 임베딩 스페이스에서도 가깝다."를 만족시키기 위함이죠. 이는 실제로 representation learning을 학습하기 위한 목적 함수로 사용됩니다. 기존 그래프에서 유사도가 높게 측정된 노드 쌍의 벡터간 내적 결과가 크게 되도록 학습합니다.

벡터로 표현된 노드는 내적을 통해 유사도를 알 수 있지만, 기존 그래프의 노드 간의 유사도를 어떻게 정의하냐는지는 정말 중요한 문제입니다. 정말 간단하게는 아래와 같이 생각할 수 있는데요.
- 연결되어 있는 노드
- 이웃을 공유하는 노드
뒤의 챕터에서 random walks라는 알고리즘을 통해 노드 유사도를 정의하는 법, 어떻게 임베딩을 유사도에 맞게 최적화 하는지 다룰 것입니다.
현재까지 설명한 노드 임베딩은 별도의 라벨 혹은 피쳐가 특정되지 않았기 때문에 unsupervised/self-supervised 라고 할 수 있기 때문에 task independent하다고 할 수 있습니다. 즉, 어느 task든 자유롭게 사용 가능하다는 것이죠.
'인공지능공부 > 그래프' 카테고리의 다른 글
| [Stanford/CS224W] 3. node embeddings(3) : 전체 그래프 임베딩 (0) | 2023.03.08 |
|---|---|
| [Stanford/CS224W] 3. node embeddings(2) : 노드 임베딩을 위한 랜덤 워크 접근 방식 (0) | 2023.03.07 |
| [Stanford/CS224W] 2. tradition-ml(3) : 전통적인 그래프 레벨 피쳐와 그래프 커널 (0) | 2023.03.02 |
| [Stanford/CS224W] 2. tradition-ml(2) : 전통적인 링크 레벨 작업과 피쳐 (0) | 2023.02.28 |
| [Stanford/CS224W] 2. tradition-ml(1) : 전통적인 노드 레벨 작업과 피쳐 (0) | 2023.02.25 |
