활성화 함수란?
신경망에서입력 신호의 총 합을 출력 신호로 변환하는 함수입니다. 퍼셉트론은 인간의 뇌의 뉴런을 모방하여 만든 것입니다. 뉴런이 말단에서 다음 뉴런으로 전달될 때, 어떠한 임계 값을 기준으로 신호가 전달된다고 합니다. 쉽게 말해서, 퍼셉트론은 뉴런처럼 입력 받은 수치들을 계산하고, 출력하기 전에 활성화 함수를 거쳐 출력에 변화를 줍니다. 이제 활성화 함수에 종류에 대해서 알아봅시다.
(1) 계단 함수

계단함수는 활성화 함수중에 가장 간단한 함수입니다. 특정한 값을 입력받았을때, 값이 0이하 즉, 음수이면 무조건 0을, 0초과이면 1을 출력해 주는 함수입니다.
def step(x):
return x > 0코드도 아주아주 간단합니다.

계단 함수
계단 함수는 그래프에서 보이는 것 처럼, 굉장히 극적으로 모양이 변합니다. 따라서 데이터의 손실이 발생할 가능성이 굉장히 높아집니다. 따라서 초기에는 많이 사용되었지만, 현재는 많이 사용되지 않습니다. 또한 불연속 함수이기 때문에 미분이 불가능합니다. 따라서 딥러닝 모델을 학습하는데 어려움이 있습니다.
(2) 시그 모이드 함수(sigmoid function)

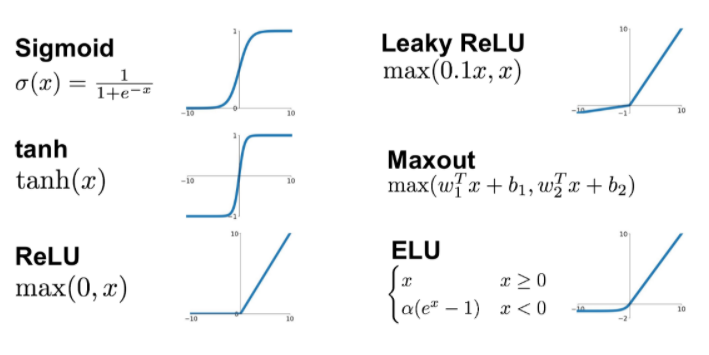
시그 모이드 함수는 S자형 곡선(시그모이드 곡선)을 갖는 함수입니다. 이 함수는 계단 함수의 단점을 보완하고자 등장한 함수입니다.
import numpy as np
def sigmoid(x):
return 1 / (1 + np.exp(-x))코드는 numpy 라이브러리 안에 있는 exp를 사용하면 쉽게 구현할 수 있습니다. 이제 그래프를 한번 그려보겠습니다.

시그모이드 함수
계단함수와 다르게 곡선을 그리는 연속된 함수라는 것을 확인할 수 있습니다. 또한 0과 1로만 출력되는 것이 아닌, 0과 1 사이의 실수로 구성되어있기 때문에, 정교한 수를 전달할 수 있고, 데이터의 손실 또한 줄어들었습니다. 하지만 시그모이드 함수는 vanishing gradient라는 문제를 발생시킵니다. 즉, 입력 값이 무한대로 커진다고 하더라도, 모델의 계층이 많을수록 gradient값이 0에 수렴하게 되어버립니다. (시그 모이드의 모든 값은 1보다 작은 수를 가지기 때문에, 계층이 많을수록 0.xxx끼리 계속 곱해지게되고, 결국에는 0에 수렴해버립니다.) 또한 데이터의 중심이 0이 아니기 때문에, 함수로 들어오는 데이터가 항상 양수인 경우, gradient는 모두 양수 또는 음수가 됩니다. 따라서 gradient를 업데이트 할 때, 지그재그로 변동하는 문제점이 발생합니다. 따라서 학습이 느려지고, 효율성이 감소합니다.
※ vanishing gradient가 뭔가요?
딥러닝은 기울기 조정해 가며, 적절한 파라미터 값을 찾아 다니는데, 앞서 말한것 처럼 은닉층이 많게 되면, 1 미만의 값들이 계속 곱해지기 때문에, 결국 기울기가 0이 되어버리는 기울기 소멸 문제가 발생하게 됩니다. 이 문제가 바로 vanishing gradient입니다.
(3) 하이퍼볼릭 탄젠트 함수(tanh function)

시그 모이드 함수를 보완하고자 나온 함수입니다.
import numpy as np
def sigmoid(x):
return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))
하이퍼볼릭 탄젠트 함수
tanh는 0~1사이의 값이 아닌, -1~1사이의 값을 출력해주는 함수입니다. 따라서 시그모이드와의 차이점은 데이터의 평균이 0.5가 아닌 0이라는것 밖에 없습니다. 이러한 점은 앞서 말한 데이터 중심이 0이 아니여서 발생하는 문제들을 해결했습니다. 하지만 여전히 vanishing gradient문제는 존재하게 됩니다.
(4) ReLU 함수
가장 많이 쓰이고 있는 활성화 함수입니다. 0 이상일 경우에는 그 수를 그대로 출력해주고, 0 이하일 경우에는 0을 출력하는 함수입니다.

import numpy as np
def relu(x):
return np.maximum(x,0)
렐루 함수
ReLU는 0과 1사이가 아니기 때문에, 0 이하의 정보는 과감하게 무시해버리죠! 따라서 sigmoid, tanh에서 발생하는 vanishing gradient문제가 해결됩니다. 따라서 은닉층이 많이 쌓인다고 하더라도, 원활한 학습이 가능해집니다. 그리고 exp()를 사용하지 않기 때문에 연산 속도 또한 엄청 빠르다고 합니다. 하지만 ReLU함수는 0 이하의 값들에 대해서는 마땅한 대응을 하지 못합니다.
(5) Leakly ReLU 함수
앞서 언급한 0 이하의 값들에 대해서 대응을 하지 못하는 ReLU의 단점을 보완한 함수입니다.

import numpy as np
def leakly_relu(x):
return np.maximum(0.01*x,x)
양수는 x에 맞게, 음수는 0.01x에 맞게 출력을 내보내는 함수입니다. 음수일 때, 수에 대해서 대응을 할 수 있게 되는 것을 빼면 기존의 ReLU와 같은 특징을 가집니다.
(6) ELU 함수
이 함수 또한 앞서 언급한 0 이하의 값들에 대해서 대응을 하지 못하는 ReLU의 단점을 보완한 함수입니다.

import numpy as np
def elu(x,alpha):
return alpha*(np.exp(x)-1) if x <= 0 else x
마찬가지로, 양수는 x에 맞게, 음수는 a*(ex-1)에 맞게 출력을 내보내는 함수입니다. 음수일 때, 수에 대해서 대응을 할 수 있게 되는 것을 빼면 기존의 ReLU와 같은 특징을 가집니다.
(7) PReLU 함수
ELU와 거의 유사하지만, PReLU가 조금 더 먼저 제안되었고, exp를 사용하지 않는다는 점에서 차이가 있습니다.

import numpy as np
def prelu(x,alpha):
return np.maximum(alpha*x,x)
※그럼 Leakly ReLU, PReLU, ELU의 차이점은 뭔가요?
0미만일 경우 Leakly ReLU, PReLU는 선형적이고, ELU는 비선형적이라는 점입니다. 또한 ELU는 exp를 사용하기 때문에, 계산량이 증가해 조금더 학습이 느려집니다. 또한 Leakly ReLU는 음수일 때, 기울기가 정해져있지만, PReLU는 기울기를 학습합니다.
(8) Maxout 함수
maxout 함수는 앞서 나온 ReLU의 단점을 보완하고, 장점은 그대로 가져온 함수입니다. 연결된 두 개의 뉴런 값 중 큰 값을 사용하는 함수이죠. 실제로 성능도 제일 좋다고 합니다. 하지만 이 함수는 계산 량이 복잡하다는 단점을 가집니다. 하나의 뉴런당 파라미터 수가 두배가 되기 때문이죠! (아래 수식에서 wT1, wT2 모두 파라미터입니다.)

(9) Softmax 함수
조금 특별한 활성화 함수입니다. 그래프는 존재하지 않고, 결과 값을 확률로 바꿔주는 함수입니다. 보통 분류기의 마지막 계층에 설정을 해두게 되는데, 만약 분류해야할 클래스가 3개면, 3개의 총 합을 1로 만들어줍니다. 즉, 개, 고양이, 토끼를 분류해야한다면, (0.3, 0.4, 0.3)이렇게 확률로 바꿔주게 되고, 이 정보는 고양이로 예측하게 됩니다.
정리
계단함수부터 Maxout함수까지 정리를 해 보았는데요, 실제로 가장 많이 사용되는 함수는 ReLU입니다. Leakly ReLU, PReLU, ELU, Maxout등의 다양한 함수가 제안되었는데, ReLU의 단점을 극복했다고 해서 모두 좋은 성능을 내는 것은 아닙니다. 모델의 상황에 따라 적절한 함수를 선택하는 사용해보는것이 중요합니다. 또한 시그모이드는 사용을 권장하지 않으며, 하이퍼블릭 탄젠트 함수의 경우에도 성능이 좋게 나오지는 않는다고 합니다.
'인공지능공부 > 인공지능기본지식' 카테고리의 다른 글
| [AI 기본 지식] 손실함수의 모든 것 (0) | 2023.03.22 |
|---|---|
| [AI 기본 지식] 역전파의 모든 것 (4) | 2021.04.16 |
| [AI 기본 지식] 최적화 함수의 모든 것(2) (0) | 2021.04.16 |
| [AI 기본 지식] 최적화 함수의 모든 것(1) (1) | 2021.04.16 |
