(7) RMSProp(Root Mean Square Propagation)
AdaGrad는 학습 시간이 길어질수록 학습률이 0에 수렴하게 된다는 문제점이 존재했었죠. RMSProp는 이러한 문제점을 해결하고자 제시된 방법입니다. RMSProp는 과거의 모든 기울기를 더하는 것이 아니라, 먼 기울기는 서서히 잊고, 새로운 기울기 정보를 크게 반영합니다.

수식을 보면 새로운 하이퍼 파라미터인 p가 추가된 것을 볼 수 있습니다. p가 작을수록 가장 최신의 기울기를 더 크게 반영합니다. 이로 인해서 이제 기울기가 무한히 커지는 것을 막을 수 있습니다.
(8) AdaDelta(Adaptive Delta)
AdaDelta역시 AdaGrad의 문제점을 해결하기위해 제시된 방법입니다. AdaDelta는 기울기의 이동 평균을 구합니다. 쉽게 말하면 AdaGrad는 0번째 단계부터 제곱합을 누적해 나갔는데, 여기서 누적해 나가는 단계 수를 w로 제한시켜버리는 방법입니다.

보기 굉장히 복잡해보여서, 기울기를 gi로 치환하겠습니다.

여기서 E[]는 이동 평균을 뜻합니다. 이를 AdaGrad의 업데이트 파라미터 업데이트식에 대입해주면 두번째 식과 같습니다. 이때, 분모를 보면 제곱평균제곱근(root mean square)형태이기 때문에 RMS[]로 나타냅니다. 따라서 세 번째 식처럼 변경될 수 있습니다.
AdaDelta는 여기서 더 나아가 학습률을 설정하지 않게 하도록 아래와 같이 정의하였습니다.

따라서 이를 아래처럼 나타낼 수 있습니다.

위의 첫번째 식을 아래처럼 변경해 줄 수 있습니다. 여기서 파라미터의 변화량, 즉 Δxi는 알 수 없기 때문에, Δxi-1로 근사하여, 최종 식을 아래와 같이 나타낼 수 있습니다.

따라서 결국 Adadelta에서는 p값만 설정해 주면 됩니다. 일반적으로 0.95를 사용한다고 합니다.
(9) Adam(Adaptive Moment Estimation)
모멘텀 방법과 RMSProp방법을 합친 방법입니다. 모멘텀은 속도를 뜻하는 하이퍼 파라미터 v를, RMSProp에서는 h를 이용하여 최적화하였습니다. 이 방법들은 처음에 0으로 초기화되면, 가중치가 학습 초반에 0으로 편향되는 문제가 존재합니다. Adam은 이러한 문제를 해결하고자 제안되었습니다. Adam은 1차 모멘텀 m(평균), 2차 모멘텀 v(집중되지 않은 분산)를 이용하여 최적화를 하였고, 수식은 아래와 같습니다.

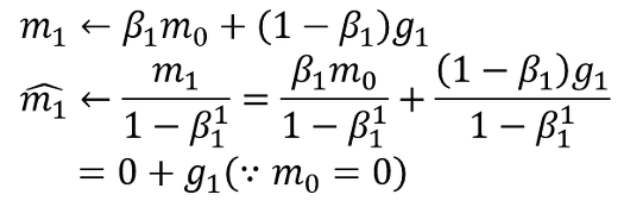
예시로 첫 번째 항을 계산해보면, m0이 0일때(처음에 0으로 초기화 될때), m1=g1이 되기 때문에, m1 = 0.1*g1(∵β1 = 0.9)이 되어, 앞서 발생하던 문제점이 해결되었습니다.

두 번째 항부터는 뒤로 갈수록 최신 기울기가 전체 평균에 10% 영향을 주고, 이는 가중이동평균 목적에 부합하다고합니다. 따라서 최종 식은 아래와 같습니다.

여기서 분자가아닌 분모에 v를 둔 이유는 v는 제곱을 하기 때문에, 값이 무조건 커지게 되고, 학습할 때 step이 너무 크지 않게 설정하기 위해 m < v인 조건을 이용했습니다.


'인공지능공부 > 인공지능기본지식' 카테고리의 다른 글
| [AI 기본 지식] 손실함수의 모든 것 (0) | 2023.03.22 |
|---|---|
| [AI 기본 지식] 역전파의 모든 것 (4) | 2021.04.16 |
| [AI 기본 지식] 최적화 함수의 모든 것(1) (1) | 2021.04.16 |
| [AI 기본 지식] 활성화 함수의 모든 것 (0) | 2021.04.16 |
