역전파란?
역전파는 오차 역전파법, 오류 역전파 알고리즘 이라고도 하며, 동일 입력층에 대해 원하는 값이 출력되도록 각 계층의 가중치를 조정하는 방법으로 사용됩니다. 즉, 예측값과 실제값의 차이인 오차를 계산하고, 이것을 다시 역으로 전파하여 가중치를 조정합니다. 이때, 역전파 과정에서는 최적화 함수를 이용합니다.
역전파를 이해하기 위해서는 인공신경망이 어떻게 가중치를 조정하는지 원리부터 알아야합니다.

위와 같이 1개의 입력층, 1개의 은닉층, 1개의 출력층이 존재합니다.(각 계층에 뉴런은 2개씩) 이제 이 신경망을 학습시켜봅시다.
(1) 순전파(forward propagation)
순전파는 입력받은 데이터를 각 가중치와 곱하여 출력을 뽑아내는 과정입니다.

먼저 입력층에서 입력을 받아 은닉층으로 전달되면, 데이터는 아래와 같이 계산됩니다.

이제 도착한 뉴런에서 활성화 함수를 계산해 줍니다. 여기서는 sigmoid를 사용한다고 가정하겠습니다.

위와 같이 활성화 함수를 통해 은닉층의 각 출력 값을 뽑아냅니다. 이후, 출력층으로 전달하기 위해 가중치들을 곱하여 전달해 줍니다. 식은 아래와 같습니다.
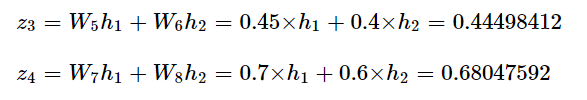
입력층에서 은닉층으로 전달될때와 같은 수식을 가집니다. 위의 값을 입력받은 출력층에서는 이후 활성화 함수를 통해 최종 값을 출력하게됩니다.

이제 최종 출력값과 실제 값을 비교해 봅시다. 이부분은 마치 우리가 수학문제를 열심히 푼 다음에 답지를 보고 채점하는 것과 같습니다.
먼저 o1의 경우 예측 값이 약 0.6인데, 실제값은 0.4죠. 약 0.2의 오차가 존재합니다. o2같은 경우 0.66을 예측하였는데, 실제값은 0.6입니다. 약 0.06의 오차가 존재하네요. 신경망 내에서는 이런 오차값들을 다루기 위해 오차 함수를 이용합니다. 오차 함수는 오차를 계산기 위한 손실함수(loss function)입니다. 손실 함수에 대한 이야기는 다음 포스팅에서 다루기로 하고, 여기서는 평균 제곱 오차 MSE를 사용하겠습니다. MSE는 실제값과 출력값의 차이를 제곱한 뒤, 2로 나누는 방법입니다. 즉, 위의 예로 오차를 구하면 아래와 같습니다.

위의 방법이 바로 MSE를 적용하여 각 뉴런의 오차를 구한 식입니다. 따라서 신경망 전체의 오차는 아래와 같습니다.
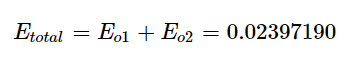
자 이제 이 값을 토대로 역전파 시키면서, 각 가중치 값을 업데이트 시켜보겠습니다.
(2) 역전파(backpropagation)
역전파는 말 그대로 순전파의 반대방향으로 전파시키는 방법입니다. 즉, 순전파는 입력층부터 차례로 계산해가며 출력층까지 나아갑니다. 역전파는 출력층으로부터 입력층까지 역으로 나아갑니다. 먼저 업데이트가 필요한 가중치는 W1,W2,W3,W4,W5,W6,W7,W8로 총 8개 입니다. 이제 역전파를 시작해 보겠습니다.

출력층 부터 시작하기 때문에, 먼저 업데이트 되는 가중치는 W5,W6,W7,W8입니다. 가중치를 업데이트 하기 위해서는 최적화 함수가 필요한데, 여기서는 단순히 경사 하강법을 이용하겠습니다. 경사 하강법을 이용하기 위해서는 오차에 대한 기울기가 필요합니다. 예를 들어서 W5를 업데이트 하려면 W5에 대한 미분을 진행해야 합니다.

즉, 미분 연쇄 법칙에 따라 위와 같이 풀어서 쓸 수 있습니다. 오른쪽 항의 세 값을 손실 함수로 부터 만들어보겠습니다.

전체 오차는 위의 식으로 구할 수 있죠? 이제 두 항을 o1에 대한 미분을 진행해 봅시다.

위와 같은 값을 얻을 수 있습니다. 오른쪽의 첫 번째 수식에서 target과 output은 모두 o1를 포함하기 때문에, 항이 사라지지 않았고, 두 번째 수식에서는 o1이 존재하지 않기 때문에 상수취급을 당해 사라졌습니다.

자 이제 식을 계산해 보면 다음과 같이 나옵니다. 이제 z3으로 미분한 구간을 계산합니다. 먼저 o1에 대한 식을 가져와보겠습니다.

이제 z3으로 미분을 해야합니다. 여기서, sigmoid가 어떻게 생겼는지 다시 한번 확인해 봅시다.

위의 값을 미분하면 어떤 값이 나올까요?

위와 같이 sigmoid함수 f(x)를 미분하면 f(x)(1-f(x))를 얻는 것을 확인할 수 있습니다. 이를 적용하여 z3으로 미분해봅시다.

여기서 o1의 값을 알 수 있기 때문에 다음과 같은 값을 얻게됩니다.
마지막으로 W5에 대한 미분을 해보겠습니다. 이를 위해 z3수식을 살펴보겠습니다.

이제 W5에 대한 미분을 해보겠습니다.

h1값은 알고 있기 때문에, 다음과 같은 값을 얻을 수 있습니다. 이제 모든 값을 구했기 때문에, 이 값들을 모두 곱해주면 됩니다.

이제 경사 하강법을 이용하여 가중치를 업데이트 해줍시다. 여기서 학습률 α는 0.5라고 합니다.
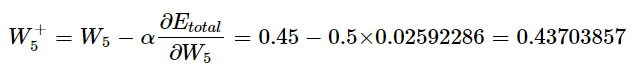
이 식이 왜 나오는지 모르겠다! 하시는 분들은 최적화함수 포스팅을 참고해주세요. 따라서 W5는 0.437이라는 갑으로 업데이트됩니다.
같은 방법으로 가중치 W6,W7,W8를 업데이트 해주시면 됩니다.

자 이제 은닉층으로 넘어가 보겠습니다. 위의 과정을 모두 거쳤다면, 아래의 그림에 표기된 부분은 업데이트가 된 상태일것입니다.

이제 W1,W2,W3,W4에 대한 가중치 업데이트를 해보겠습니다. 먼저 W1를 업데이트 시켜보겠습니다. 위에 했던 과정과 동일하게, 전체 오차를 W1로 미분시켜줍니다.

오른쪽 항의 첫 번째 식은 아래와 같이 얻을 수 있습니다.

여기서 오른쪽 첫번째 식에 대해서 항분해, 계산을 하면 아래와 같습니다.

같은 원리로 두 번째 식을 구하면 아래와 같이 나옵니다.

따라서 dEtotal/dh1은 아래와 같은 값을 얻습니다.

다음으로 dh1/dz1에 대해서는 아래 식을 미분해서 구할 수 있습니다.

앞에서 했던 계산이죠? sigmoid를 미분하면 f'(x) = f(x)(1-f(x))가 되기 때문에 아래와 같이 값을 구할 수 있습니다.

또한 dz1/dW1을 위해 아래의 식을 W1에 대해 미분해봅시다.


따라서 업데이트 하기 위한 모든 값들은 다 구했습니다.

이제 이 값과 최적화 함수를 이용하여 W1를 업데이트 해봅시다.

W2,W3,W4과정 모두 동일하게 진행해 주시면 됩니다.

'인공지능공부 > 인공지능기본지식' 카테고리의 다른 글
| [AI 기본 지식] 손실함수의 모든 것 (0) | 2023.03.22 |
|---|---|
| [AI 기본 지식] 최적화 함수의 모든 것(2) (0) | 2021.04.16 |
| [AI 기본 지식] 최적화 함수의 모든 것(1) (1) | 2021.04.16 |
| [AI 기본 지식] 활성화 함수의 모든 것 (0) | 2021.04.16 |
