728x90
반응형
인공지능을 이해하기 위해서는 선형대수를 알고 계셔야 합니다.
선형 대수?
선형 대수란 "선형 방정식을 풀기 위한 방법론을 배우는 학문"이라고 할 수 있습니다. 이게 무슨 소리일까요?
예를 들어 bx + c = 0 이라는 방정식이 있다고 가정합시다. 앞의 방정식을 성립하는 x를 찾는 것을 뜻합니다.
그럼 왜 이름이 선형 대수학일까요?
먼저 선형이란 어떤 방정식의 입력이 바뀌지 않는 방정식을 뜻합니다. 즉, 입력 변수가 1차인 것을 뜻합니다.
y = 2x + 2 라는 수식이 있을 때, x의 값에 2배를 한 뒤 2를 더한 값이 결과가 됩니다.
하지만 y = 2x2 + 2라는 수식이 있을 경우 x값 자체를 제곱해 버리기 때문에 x 자체가 변해버립니다.
즉, 선형으로 일정한 규칙으로 증가하는게 아니라 큰 값을 넣을수록 어마어마하게 커져버리죠!
이 설명이 헷갈리신다면 그래프를 한번 그려보는 것도 좋습니다.

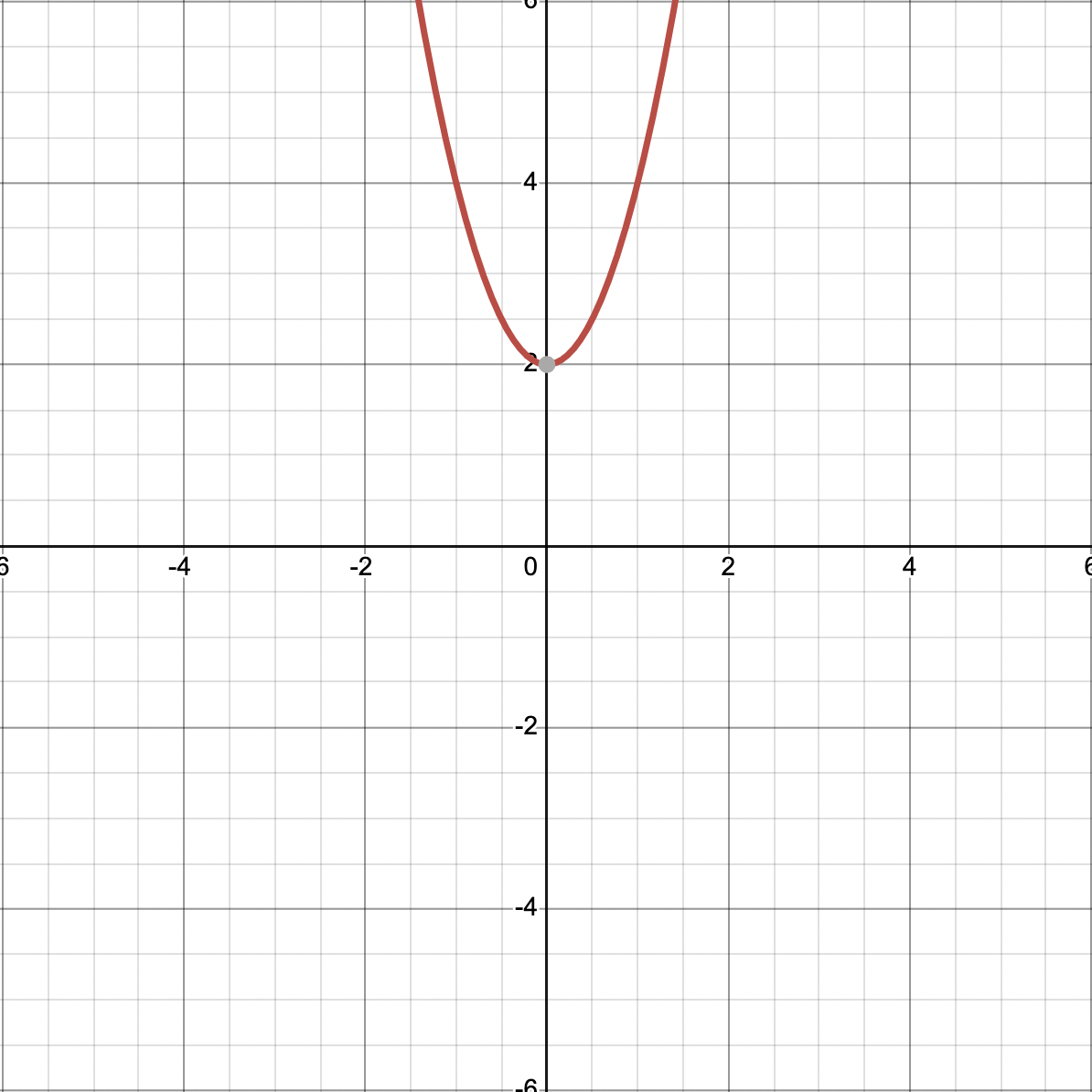
y = 2x + 2는 좌측 y = 2x2 + 2는 우측 입니다. 무엇이 선형인지 바로 알아보시겠죠?
이번엔 대수입니다. 대수에서 "대"는 "대신할 대(代)"를 사용합니다.
무언가가 숫자를 대신하여 해를 구한다라는 것인데, 여기서 대신하는 것이 바로 선형 방정식입니다.
즉, 선형대수는 "선형 방정식만으로 해를 구하는 학문이다"라고 할 수 있습니다.
이때 계산에서 행렬과 벡터의 개념이 등장합니다.
벡터의 정의와 연산은 다음 포스팅에서 다루겠습니다!
반응형
