그래프란?
그래프는 간단히 말해서 점(node)과 선(edge)으로 이루어진 하나의 데이터 형태입니다. 기존 우리가 알던 배열로 이루어진 데이터와는 다른 형태입니다. 그래프는 두 점(node) 사이의 관계나 상호작용을 나타내는 데이터를 다룰때 주로 사용됩니다.
예를들어보겠습니다. 페이스북에 A, B, C 세 사람의 친밀도를 데이터로 나타내 봅시다.
만약 그래프 형태의 데이터를 사용하지 않는다면 우리는 이러한 형태의 데이터로 표현할 수 있을 것입니다.

이렇게 표현하면 모든 A, B, C를 조합해야하기 때문에, 각각 두번씩 중복되어 사용됩니다.
이번에는 그래프로 한번 표현해 보겠습니다.

모든 사람의 조합을 찾지 않고도 아주 간결하게 표현할 수 있습니다. 따라서 그래프는 노드 사이의 관계를 표현할 때 아주 효과적인 데이터 표현방법이라고 할 수 있습니다.
그럼 이제 그래프를 어떻게 정의하는지 한번 살펴보겠습니다.

위의 그림에서 사람을 점(node or vertex)이라고 하며, 사람 사이의 관계를 선(edge)이라고 표현합니다.
하나의 그래프는 수식으로 G = (N,E) 또는 G = (V,E)라고 표현합니다. 여기서 G는 그래프, N과 V는 각 점의 집합, E는 선의 집합입니다.
그래프의 특징
1. 비정형 데이터이다. (=유클리드 공간에 있지 않다.)
일반적으로 배열을 생각해보면 굉장히 규칙적으로 생겼죠. 하지만 그래프는 규칙적이지 않습니다.
위에서 설명했던 것 처럼 그래프의 정의는 단순히 G = (N,E)이기 때문에, 점의 집합과 선의 집합이 같다면 같은 그래프입니다.

여기서 더 나아가면, 우리는 위의 그래프를 좌표계에 표현할 수 없다는 것을 알 수 있습니다.
일반적으로 정형 데이터들은 유클리드 공간(=좌표계)에 표현하는데, 그래프는 유클리드 공간에 표현할 수 없습니다.
2. 추상적인 데이터 표현에 적합하다.
관계나 상호작용같이 추상적인 개념을 다루는데 아주 적합합니다. 복잡한 문제를 간단하게 표현할 수 있게 해줍니다.
예를 들어 우리는 'A, B는 연인 관계이다'를 알고 있을때, '연인'이라는 관계를 추상적으로 생각하고있죠. 하지만 이 말을 그래프로 그린다면, 추상적인 표현의 시각화가 가능합니다. 따라서 데이터를 더 잘 이해할 수 있겠죠!
그래프의 종류
그래프의 종류를 결정하는 것은 "선"입니다.
주로 선에 방향이 있는지 없는지, 가중치가 있는지 없는지에 따라 그래프 종류가 달라집니다.
1. 그래의 방향이 없는 Undirected Graph
말 그대로 그래프 방향이 없고, 연결성만 있는 그래프입니다.
2. 그래프의 방향이 있는 Directed Graph
그래프의 방향이 존재하는 그래프입니다.
3. 그래프에 가중치가 있는 Weighted Graph
그래프의 선에 가중치가 존재하는 그래프입니다.
4. 그래프에 가중치가 없는 Unweighted Graph
그래프에 가중치가 없고, 연결성만 있는 그래프입니다.
자 여기서 가중치와 방향성을 서로 섞어서 사용할 수 있습니다. 즉, 방향성은 없으나 가중치는 있는 그래프, 방향성도 있고 가중치도 있는 그래프 등등 총 4가지의 그래프를 만들 수 있습니다.

추가적으로 자기 자신에게 가는 선을 그을 수 있는데, 이것을 Self Loop라고 합니다.
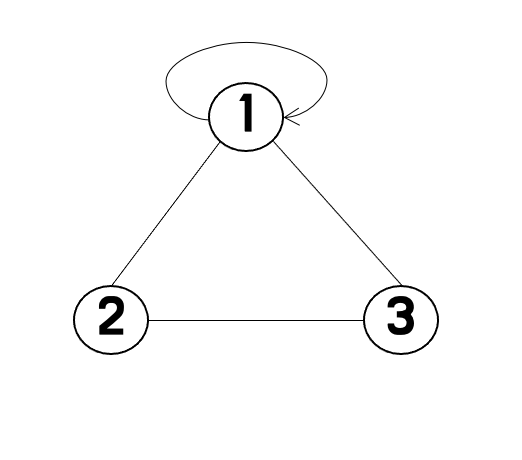
위의 그래프는 "Undirected Graph이면서 Unweighted Graph이고, Self Loop를 가졌다"라고 할 수 있습니다.
'인공지능공부 > 그래프' 카테고리의 다른 글
| [Stanford/CS224W] 2. tradition-ml(2) : 전통적인 링크 레벨 작업과 피쳐 (0) | 2023.02.28 |
|---|---|
| [Stanford/CS224W] 2. tradition-ml(1) : 전통적인 노드 레벨 작업과 피쳐 (0) | 2023.02.25 |
| [Stanford/CS224W] 1. intro(3) : 그래프 표현의 선택 (0) | 2023.02.25 |
| [Stanford/CS224W] 1. intro(2) : 그래프 ML의 응용 (1) | 2023.02.24 |
| [Stanford/CS224W] 1. intro(1) : 그래프가 필요한 이유 (1) | 2023.02.23 |
