스탠포드 강의를 듣고 정리한 내용입니다.
지난 포스팅에서는 페이지 랭크 알고리즘에 대해서 배워보았습니다.
이번 포스팅에서는 페이지 랭크 문제점과 어떻게 해결해 나가는지 알아보겠습니다.
PageRank Remind
페이지 랭크에 대한 기본 개념들은 지난 포스팅을 참고해 주시길 바랍니다.
우리는 앞에서 페이지 랭크의 수식을 다음과 같이 정의했었죠.

말로 풀어서 설명하자면, t+1번째 노드의 중요도는 t번째 나에게로 들어오는 모든 노드의 중요도의 합과 같습니다.
그래서 이 과정을 언제까지 하냐 살펴보면,

다음과 같이 이전 중요도와 임계값 이하로 차이가 날 때까지 위의 과정을 반복합니다.
위의 과정을 matrix로 표현하면 아래와 같은 수식을 얻을 수 있습니다.

초기 각 노드의 중요도는 1/노드 수이고, r(t+1) = M*rt을 계속 반복합니다.
위의 수식과 동일하게 현재 노드와 과거 노드의 중요도의 차가 임계값 미만이 될 때까지 반복합니다.

결국 표현 방법만 조금 다를 뿐 같은 수식이죠.
여기서 두 가지 문제점이 발생할 수 있습니다.
1. 모든 페이지(노드)가 같은 그룹 내에만 있을 수 있습니다. 이를 spider trap 이라고 합니다.
결국에 spider trap은 모든 중요도들을 다 흡수해 버립니다.

위의 그래프를 보시면 a에서 b로 가는데 b는 자기 자신을 가르키고 있기 때문에, 모든 중요도를 계속 흡수합니다.

따라서 계속 반복하면 할수록 a의 중요도는 0, b의 중요도는 1에 수렴하게 됩니다.
2. 몇몇의 페이지(노드)들은 그 누구도 가르키지 않는 dead end일 수 있습니다.
이렇게 될 경우 중요도가 새어나갈 수 있죠(leak out).

위와는 반대되는 상황으로 a에서 b로 갔는데, b가 아무것도 가르키고있지 않습니다. 따라서 a에게 들어오는 중요도가 없기 때문에 점점 낮아지고, 이를 받는 b 또한 낮아집니다.

결국엔 이렇게 모두 0에 수렴하게 되어버립니다.
위의 문제들은 어떻게 해결해야 할까요?
1. spider traps의 해결 방법
매 스탭마다 랜덤하게 surfer를 두 가지 옵션으로 이동하게 만들어 줍니다.
- β의 확률로 기존 링크를 따라감
- 1-β의 확률로 랜덤하게 페이지를 순간이동함
이 때 β는 0.8~0.9로 설정하는 것이 좋다고 합니다.

기존에는 왼쪽 그래프처럼 실선으로만 이동이 가능했지만, 위의 조건들을 붙인다면 오른쪽 그래프의 점선처럼도 이동이 가능해집니다.
2. dead end의 해결 방법
spider trap과 비슷한 방법인데요. 막다른길을 만났을 경우 즉, dead end를 만났을 경우 텔레포트합니다.

즉 기존에는 왼쪽과 같이 그래프, matrix로 표현될 수 있었는데요. 자세히 보시면 m행의 합은 1이 되어야 하는데 0입니다!
이를 아무 노드에나 갈 수 있도록 텔레포트하게 만들어주면, m열의 각 행들이 1/노드 수가 됩니다. 즉, m열을 확률적으로 만들어 주는 것이죠.
google's solution
기존의 페이지 랭크 문제점을 해결하고자 구글의 솔루션이 등장합니다.
사실상 위의 개념과 크게 차이는 없는데요.
이 방법에서는 매 스탭마다 아래의 두 옵션을 추가해 줍니다.
- β의 확률로 기존 링크를 따라감
- 1-β의 확률로 랜덤하게 페이지를 순간이동함
그렇다면 우리는 식을 아래와 같이 변형해 줄 수 있습니다.

이 식을 matrix로 표현하면 아래와 같습니다. 여기서 G는 google matrix라고도 하죠!

β는 위에서와 동일하게 0.8~0.9으로 설정해 줍니다.
여기서 만든 google matrix인 G를 아래와 같이 계속 곱해주면 됩니다.

예를 한번 들어볼까요?

위와 같은 그래프가 하나 있다고 합시다. β는 0.8로 설정할 경우 아래와 같이 matrix를 얻을 수 있습니다.
(왼쪽 matrix는 정상적으로 링크를 따라 갈 확률, 오른쪽은 점프해서 아무 노드나 갈 확률입니다!)

결국 google matrix인 G는 아래와 같습니다.

최종적으로 계속계속 곱하면 아래와 같이 각 노드별 중요도를 얻을 수 있습니다.

실제로 페이지 랭크 알고리즘의 결과를 보면,
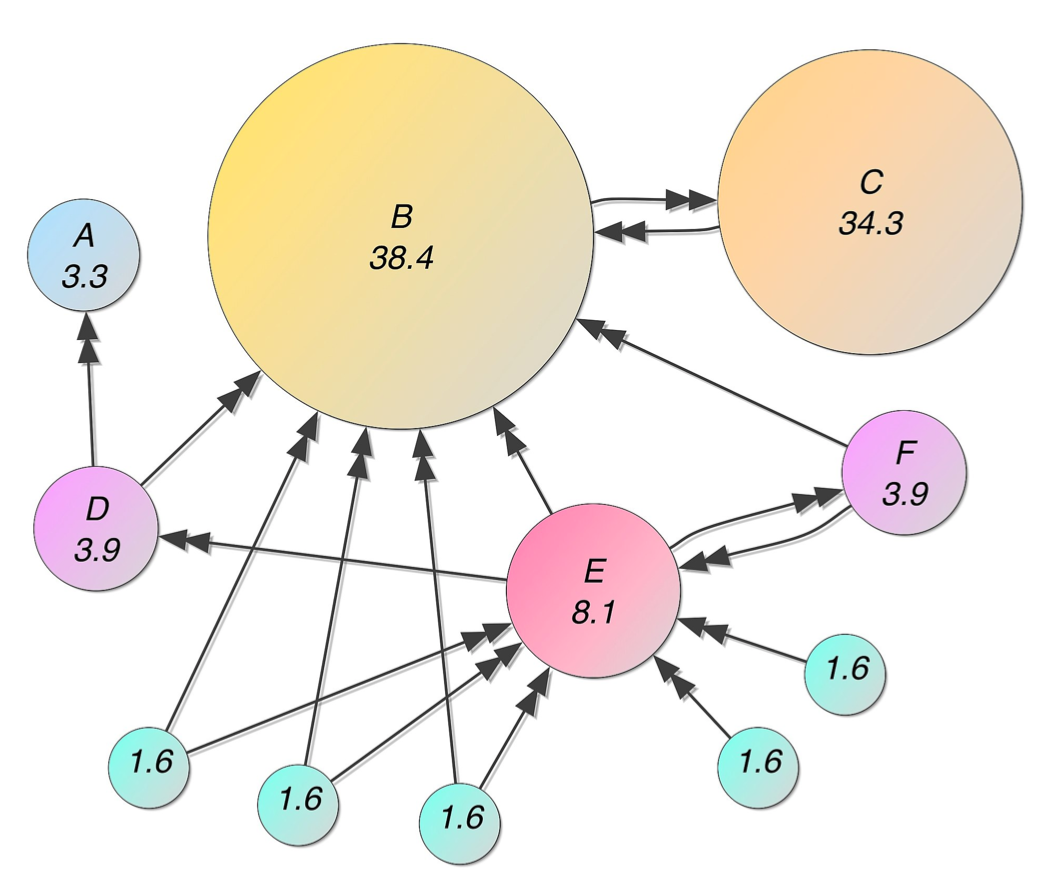
위와 같이 나타낼 수 있는데요.
초기 페이지 랭크는 중요도가 높은 페이지(노드)가 참조를 하고 있다면 그 페이지 역시 중요도가 커진다고 말씀드렸습니다.
C의 경우를 보시면, C로 들어오는 링크가 가장 중요도가 높은 B밖에 없음에도, 상당히 높은 중요도를 가지고 있죠!
