스탠포드 강의를 듣고 정리한 내용입니다.
지난 포스팅에서는 Personalized PageRank(PPR), Random Walk with Restarts(RWR) 알고리즘에 대해서 알아봤습니다.
페이지 랭크 알고리즘의 문제점과 해결방법을 알아 보았습니다.
이번 포스팅에서는 노드 임베딩의 Matrix Factorization에 대해서 알아보겠습니다.
Matrix Factorization

노드 임베딩 관련 예전 포스팅에서 우리는 노드 임베딩 매트릭스를 위와 같이 정의했었죠. 각 노드들은 전체 matrix의 한 행을 의미하고, 이 임베딩의 목적은 각 노드의 내적이 최대가 되는것이었습니다.
간단하게 생각하면 노드 사이의 내적(유사도)라는 것은 노드 끼리 연결되어 있는 것을 뜻하죠.
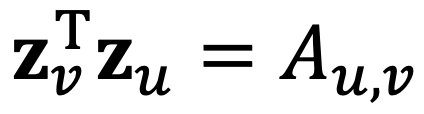
따라서 두 노드 v, u가 연결 되어 있다면 1, 연결되어 있지 않으면 0이 됩니다.
여기서 A는 adjacency matrix입니다.

이번에는 반대로 matirx A부터 생각해 봅시다. A의 요소를 하나 선택했을 때, 그 요소가 1이라면, 노드를 임베딩한 값들의 내적이 1이 되기를 원하죠!(그렇게 학습 되기를 원합니다!)

그렇다면 위의 식이 바로 임베딩의 목적이 되겠습니다. 위의 계산 식은 L2 Norm입니다!
결론 적으로 말하면, adjacency matrix인 A는 노드 행렬 Z로 쪼개질 수 있다는 것을 뜻합니다.
이것이 바로 matrix factorization이라고 합니다. 말 그대로 matrix를 분해하는것이죠!
우리가 배웠던 Deepwalk, Node2vec 같은 경우에도 matrix factorization이 가능하지만, 굉장히 복잡합니다.
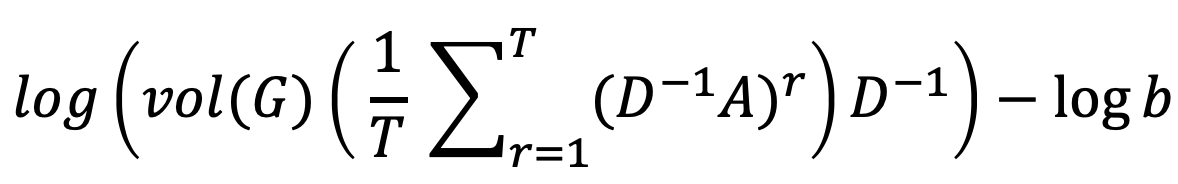

여기에는 3가지 한계점이 존재합니다.
1. 학습 데이터에 포함되지 않은 노드는 임베딩할 수 없다.
ㄴ 따라서 새로운 노드가 생기면, 처음부터 다시 실행해야합니다.

2. 구조적으로 유사한 부분을 알 수 없다.
ㄴ노드 1과 11은 매우 유사한 구조를 가지고 있죠. 이러한 구조를 알 수 없게 됩니다.

3. 노드, 간선, 그래프 피쳐를 고려하지 못한다.
ㄴDeepwalk, node2vec는 위의 피쳐들을 통합하지 않습니다.

