스탠포드 강의를 듣고 정리한 내용입니다.
지난 포스팅에서는 페이지 랭크 알고리즘의 문제점과 해결방법을 알아 보았습니다.
이번 포스팅에서는 재시작이 포함된 랜덤 워크와 개인화된 페이지 랭크에 대해서 알아보도록 하겠습니다.
앞의 포스팅에서 페이지 랭크의 해결 방법으로 모든 노드를 균일한 확률로 순간이동을 했었습니다. 여기서는 두 노드가 유사성을 전혀 고려하지 않습니다. 일반적으로 생각했을 때, 유사한 노드에 더 많이 이동해야 더 명확한 값을 가질 수 있겠죠?
Recommendation
먼저 각 알고리즘에 대해 알아보기 전에 그래프를 이용한 추천에 대해서 알아보고 가겠습니다.

다음과 같이 하나의 유저 노드가 여러개의 아이템 노드를 가질 수 있는 bipartite graph(이분 그래프)로 표현해 줄 수 있습니다.
위의 그래프는 추천에 쓰기 때문에 주된 Task는 "item Q를 구매한 유저에게 어떤 아이템을 추천해 줄 수 있는가?"입니다.
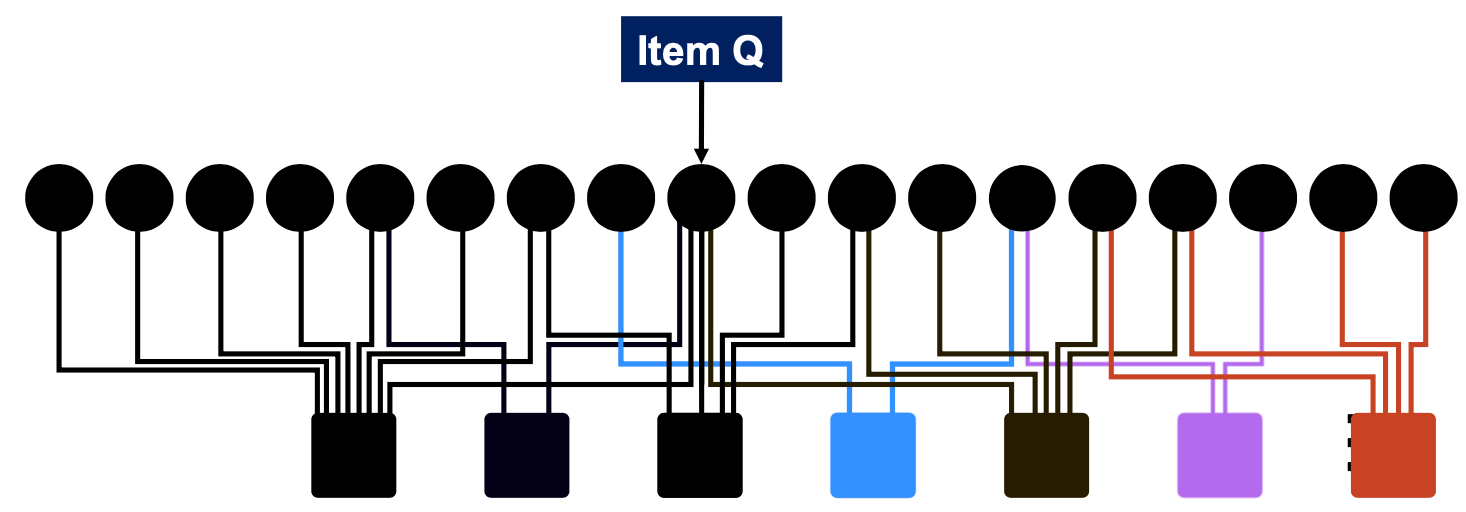
이 Task에 대해 우리가 직관적으로 생각해 볼 수 있는 것은 Q와 P를 동시에 구매한 사용자와 비슷한 특성을 가진 사용자가 Q를 구매했다면, P를 추천해 준다는 것입니다.
그렇다면 우리는 어떤 상품이 더 추천에 적합한지 알아야합니다. 즉, 기준이 되는 상품과 어떤 상품이 더 유사도가 높은지 알아내야합니다.

위와 같은 상황에서 A, A'와 B, B' 중 어느 것이 더 유사도가 높을까요?
다른 노드를 지우고 다시 살펴봅시다.

A, A'가 B, B'보다 더 짧은 경로로 이어져 있는 것을 알 수 있습니다. 따라서 A, A'가 더 가깝다(더 유사하다)고 할 수 있습니다.

그렇다면 C, C'와 비교하면 어떨까요? 딱 봐도 C, C'가 더 유사도가 높을 것임을 알 수 있습니다. (더 많은 연결이 있기 때문이죠.)
Personalized PageRank(PPR)
기존의 페이지 랭크 알고리즘에서 랜덤하게 이동하지 말고, 유사한 노드로 이동을 하자!라는 아이디어로 Personalized PageRank(PPR)이 제안됩니다.
PPR알고리즘은 다음과 같이 작동합니다.
설명에 앞서 앞의 포스팅에서 정의했던 페이지 랭크의 수식을 가져오겠습니다.

1. 시작점은 Q노드이며, 부분 노드 집합 S가 주어진다.
2. Random Walk 를 수행한다. 여기서 1-β의 확률로 부분 노드 집합 S로 돌아간다.
3. 위의 작업을 계속 반복하면서 나온 노드 방문 횟수를 벡터화한다.
결국 얻을 수 있는 것은 시작노드 Q와 다른 노드들의 유사도 벡터 입니다.
여기서 노드가 5개인 S 예를 들어 보자면 아래와 같습니다.
S = [0.1, 0, 0, 0.4, 0.5]
보시는 것처럼 0이 아닌 수로 텔레포트를 쓸 수 있겠죠?
Random Walk with Restarts(RWR)
PPR과 개념 자체는 똑같습니다. 다만 부분 노드 집합에 Q가 있다는 점에서 다릅니다.
PWR 알고리즘은 다음과 같이 작동합니다.
1.시작 점은 Q노드이며, 노드 집합 S={Q}가 주어진다.
2. Random Walk 를 수행한다. 여기서 1-β의 확률로 부분 노드 집합 S로 돌아간다. (=초기 노드 Q로 돌아간다.)
3. 위의 작업을 계속 반복하면서 나온 노드 방문 횟수를 벡터화한다.
여기서도 결국 얻을 수 있는 것은 시작노드 Q와 다른 노드들의 유사도 벡터 입니다.
여기서 노드가 5개인 S 예를 들어 보자면 아래와 같습니다.
S = [0, 1, 0, 0, 0]
PPR과 다른 점이 보이시나요? RWR에서는 시작 노드 Q만을 포함합니다. 따라서 시작 노드 값이 1이 됩니다.
지금까지 PPR, RWR 알고리즘을 살펴보았는데요.
왜 이 알고리즘들이 유사도를 표현하기에 좋은 알고리즘이라고 할 수 있을까요?
- Multiple connections
- Multiple paths
- Direct and indirect connections
- Degree of node
바로 위의 모든 요소들을 고려하기 때문입니다!
'인공지능공부 > 그래프' 카테고리의 다른 글
| [Stanford/CS224W] 5. Message Passing(1) : Message Passing and Node Classification (0) | 2023.03.17 |
|---|---|
| [Stanford/CS224W] 4. PageRank(4) : Matrix Factorization and Node embedding (0) | 2023.03.15 |
| [Stanford/CS224W] 4. PageRank(2) : 페이지 랭크 문제 해결 (0) | 2023.03.13 |
| [Stanford/CS224W] 4. PageRank(1) : 페이지 랭크 (0) | 2023.03.09 |
| [Stanford/CS224W] 3. node embeddings(3) : 전체 그래프 임베딩 (0) | 2023.03.08 |
