최근 자연어 처리의 기본에 대해 포스팅을 시작했는데요.
통계적 임베딩을 설명하는데 반드시 필요한 개념인데,
해당 포스팅에 담기에는 또 너무 길더라고요.
그래서 고유값, 고유벡터 먼저 설명한 뒤, 임베딩을 설명하려고합니다.
이번 포스팅에서 고유값, 고유벡터를 정말 쉽게 설명하려고해요.
끝까지 잘 따라와주시면 감사할 것 같습니다.
질문과 의견은 언제든지 환영합니다.

고유값(Eigenvalue)과 고유 벡터(Eigenvector)란?
선형대수 공부하면 나오는 용어이죠. 처음 배우시는 분들도 계시고 잠시 까먹으신 분들도 계실 수 있어요.
고유 벡터라고 하는 것은 방향이 변하지 않는 벡터입니다.
만약 사람이 에스컬레이터를 탄다면, 방향이 변하지 않고 쭉 가죠. 이 때 사람이 고유벡터, 이동한 거리가 고유값이라고 할 수 있어요.
즉, 고유값은 고유 벡터가 얼마나 늘어나거나, 줄어드는지 나타내는 값입니다.
반면 회전문에 사람이 지나치면 사람의 방향이 완전 바뀌어버리게 됩니다. 이 것은 고유벡터가 아닙니다.
수학적으로 행렬 A가 벡터 v에 대해 다음을 만족할 때
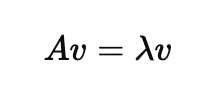
- v는 고유벡터
- λ는 고유값
이렇게 정의합니다.
의미를 살펴보면 어떠한 행렬 A가 어떤 벡터 v에 작용했을 때, 방향은 그대로이고 크기만 λ배로 변한다는 것을 의미합니다.
이 때 v, λ값은 A의 고유벡터, 고유값이라고 불립니다.
고유값과 고유 벡터 구하는 방법
그럼 고유값과 고유벡터에 대해서 알아봤으니, 이제는 어떻게 구하는지 한번 펴볼게요.
예시로 보여드리는 것이 더 쉬울 것 같아서 A행렬을 아래와 같이 정의하도록 하겠습니다.
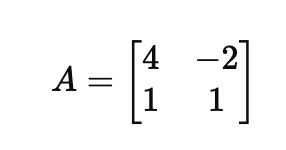
고유값, 고유 벡터를 구하기 위해서는 특성 방정식을 구해야하는데요.
만약 이 개념을 모르겠다면, 아래 펼치기를 하셔서 확인해주세요!
step1. 초기 고유벡터, 고유값을 만족하는 식
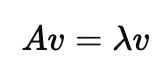
- A는 nxn행렬
- v는 nx1 벡터(고유벡터, 0이 아닌 벡터)
- λ는 고유값(스칼라)
step2. 식 변환
먼저 모든 수를 좌변으로 넘겨볼게요.
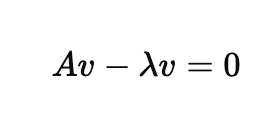
그럼 이제 공통된 벡터 v로 묶을 수 있게 되었습니다. 한번 묶어볼게요.
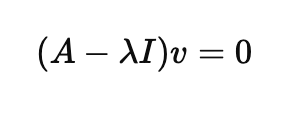
여기서 새로운 행렬인 (A-λI)라는 행렬이 나오게 됩니다.
이 행렬이 어떤 벡터 v에 대해 0벡터를 만들려면, 행렬이 역행렬이 없어야합니다.
v벡터는 0이 아닌 벡터이기 때문에, 행렬식은 다음과 같이 0이 되어야합니다.
"v벡터와 곱해져서 수식을 0으로 만들 수 있지 않나요?" 궁금 하실 수 있는데요.
앞에 설명에서도 말씀 드렸듯이, 고유벡터는 방향을 바꾸지 못합니다. 따라서 어떻게 해서든 기존 수식을 0으로 만들 수 없습니다.
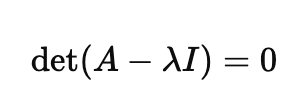
- 역행렬이 존재하려면 행렬식(det)이 0이 아니어야한다.
- 만약 det가 0이면 행렬은 특이행렬이 되어 역행렬이 존재하지 않는다.
위의 선형대수의 기본 개념들 때문에, 위의 식을 만족해야합니다.
이 식이 바로 특성방정식(Characteristic Equation)입니다.
그럼 이제 특성방정식을 적용해볼게요.
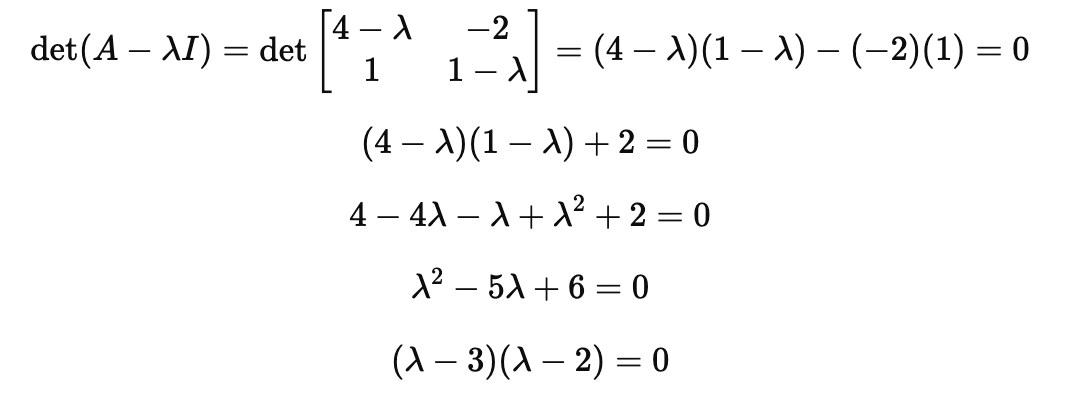
따라서 λ값은 2와 3입니다. 이 값이 바로 고유값입니다.
고유값을 구했으니, 고유벡터를 한번 구해볼게요.
고유벡터는 앞서 구한 고유값을 하나씩 넣어서 구할 수 있습니다.
λ = 3인 경우
위에서 얻은 식에 3을 대입해 볼게요.
그럼 아래와 같은 식을 얻을 수 있는데요.
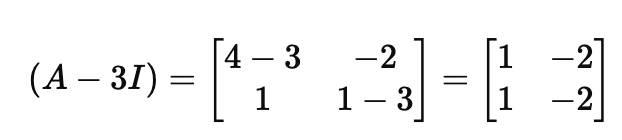
마지막으로 구한 행렬 값을 식에 대입을 해봅시다.
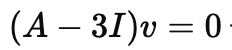
v = (x, y)라고 했을 때, x = 2y가 나오는데요.
따라서 대략적으로 다음과 같이 표현할 수 있습니다.
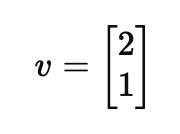
v = (-2, -1), (4, 2) 등 수많은 벡터가 될 수 있습니다. 단, 0은 안됩니다.
λ = 2인 경우
2의 값을 가질 경우에도 수식에 대입하면 행렬을 얻을 수 있어요.
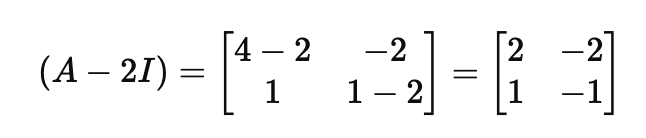
여기에서도 v = (x, y)로 정의하고 식을 구할 수 있는데요. x = y값을 얻을 수 있습니다.
즉, 정말 간단하게 나타내면 아래와 같은 값을 얻을 수 있어요.
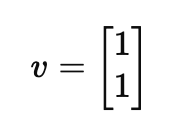
마찬가지로 v = (4, 4), (10, 10) 등 0을 제외한 수많은 벡터가 될 수 있어요.
왜 머신러닝에서 중요한가?
그럼 고유값, 고유벡터가 머신러닝에서 왜 중요한걸까요?
이 값을 알게 됨으로써 데이터의 핵심을 잘 파악하고, 복잡한 문제를 쉽게 풀 수 있기 때문입니다.
예를 들어 데이터의 핵심인 나무젓가락이 있다고 해볼게요.
여러 데이터가 표현되면서 또 다른 데이터인 고무 찰흙이 나무젓가락에 덕지덕지 붙습니다. 그럼 데이터가 점점 무거워지겠죠.
그래서 데이터의 핵심만 잘 발라내는 것이 중요합니다. 이게 바로 고유 벡터를 찾는 것이라고 할 수 있죠.
간단히 말하면, 데이터의 본질적인 특징을 잘 나타내는 방향을 찾는다고 보시면 됩니다.
추후 배울 PCA(주성분 분석) 등에서 이용됩니다.
오늘은 고유값과 고유벡터에 대해 알아보았는데요!
궁금한 점 있으면 언제든지 댓글 남겨주세요!
읽어주셔서 감사합니다.

최근 자연어 처리의 기본에 대해 포스팅을 시작했는데요.
통계적 임베딩을 설명하는데 반드시 필요한 개념인데,
해당 포스팅에 담기에는 또 너무 길더라고요.
그래서 고유값, 고유벡터 먼저 설명한 뒤, 임베딩을 설명하려고합니다.
이번 포스팅에서 고유값, 고유벡터를 정말 쉽게 설명하려고해요.
끝까지 잘 따라와주시면 감사할 것 같습니다.
질문과 의견은 언제든지 환영합니다.

고유값(Eigenvalue)과 고유 벡터(Eigenvector)란?
선형대수 공부하면 나오는 용어이죠. 처음 배우시는 분들도 계시고 잠시 까먹으신 분들도 계실 수 있어요.
고유 벡터라고 하는 것은 방향이 변하지 않는 벡터입니다.
만약 사람이 에스컬레이터를 탄다면, 방향이 변하지 않고 쭉 가죠. 이 때 사람이 고유벡터, 이동한 거리가 고유값이라고 할 수 있어요.
즉, 고유값은 고유 벡터가 얼마나 늘어나거나, 줄어드는지 나타내는 값입니다.
반면 회전문에 사람이 지나치면 사람의 방향이 완전 바뀌어버리게 됩니다. 이 것은 고유벡터가 아닙니다.
수학적으로 행렬 A가 벡터 v에 대해 다음을 만족할 때
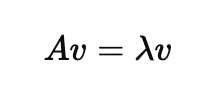
- v는 고유벡터
- λ는 고유값
이렇게 정의합니다.
의미를 살펴보면 어떠한 행렬 A가 어떤 벡터 v에 작용했을 때, 방향은 그대로이고 크기만 λ배로 변한다는 것을 의미합니다.
이 때 v, λ값은 A의 고유벡터, 고유값이라고 불립니다.
고유값과 고유 벡터 구하는 방법
그럼 고유값과 고유벡터에 대해서 알아봤으니, 이제는 어떻게 구하는지 한번 펴볼게요.
예시로 보여드리는 것이 더 쉬울 것 같아서 A행렬을 아래와 같이 정의하도록 하겠습니다.
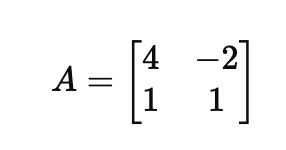
고유값, 고유 벡터를 구하기 위해서는 특성 방정식을 구해야하는데요.
만약 이 개념을 모르겠다면, 아래 펼치기를 하셔서 확인해주세요!
step1. 초기 고유벡터, 고유값을 만족하는 식
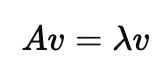
- A는 nxn행렬
- v는 nx1 벡터(고유벡터, 0이 아닌 벡터)
- λ는 고유값(스칼라)
step2. 식 변환
먼저 모든 수를 좌변으로 넘겨볼게요.
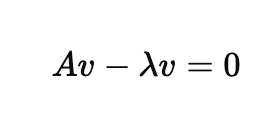
그럼 이제 공통된 벡터 v로 묶을 수 있게 되었습니다. 한번 묶어볼게요.
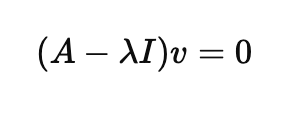
여기서 새로운 행렬인 (A-λI)라는 행렬이 나오게 됩니다.
이 행렬이 어떤 벡터 v에 대해 0벡터를 만들려면, 행렬이 역행렬이 없어야합니다.
v벡터는 0이 아닌 벡터이기 때문에, 행렬식은 다음과 같이 0이 되어야합니다.
"v벡터와 곱해져서 수식을 0으로 만들 수 있지 않나요?" 궁금 하실 수 있는데요.
앞에 설명에서도 말씀 드렸듯이, 고유벡터는 방향을 바꾸지 못합니다. 따라서 어떻게 해서든 기존 수식을 0으로 만들 수 없습니다.
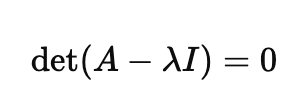
- 역행렬이 존재하려면 행렬식(det)이 0이 아니어야한다.
- 만약 det가 0이면 행렬은 특이행렬이 되어 역행렬이 존재하지 않는다.
위의 선형대수의 기본 개념들 때문에, 위의 식을 만족해야합니다.
이 식이 바로 특성방정식(Characteristic Equation)입니다.
그럼 이제 특성방정식을 적용해볼게요.
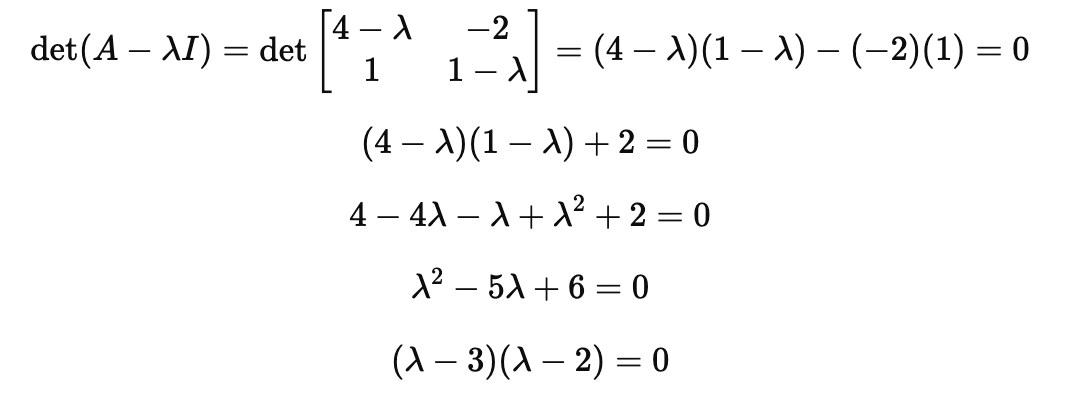
따라서 λ값은 2와 3입니다. 이 값이 바로 고유값입니다.
고유값을 구했으니, 고유벡터를 한번 구해볼게요.
고유벡터는 앞서 구한 고유값을 하나씩 넣어서 구할 수 있습니다.
λ = 3인 경우
위에서 얻은 식에 3을 대입해 볼게요.
그럼 아래와 같은 식을 얻을 수 있는데요.
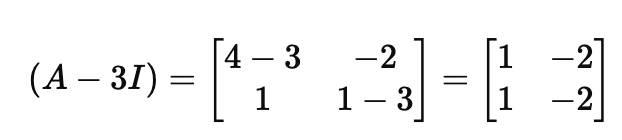
마지막으로 구한 행렬 값을 식에 대입을 해봅시다.
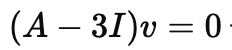
v = (x, y)라고 했을 때, x = 2y가 나오는데요.
따라서 대략적으로 다음과 같이 표현할 수 있습니다.
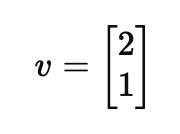
v = (-2, -1), (4, 2) 등 수많은 벡터가 될 수 있습니다. 단, 0은 안됩니다.
λ = 2인 경우
2의 값을 가질 경우에도 수식에 대입하면 행렬을 얻을 수 있어요.
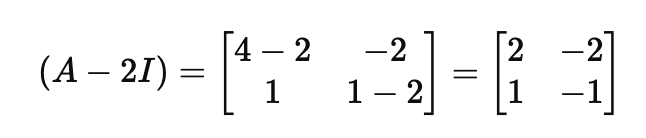
여기에서도 v = (x, y)로 정의하고 식을 구할 수 있는데요. x = y값을 얻을 수 있습니다.
즉, 정말 간단하게 나타내면 아래와 같은 값을 얻을 수 있어요.
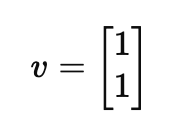
마찬가지로 v = (4, 4), (10, 10) 등 0을 제외한 수많은 벡터가 될 수 있어요.
왜 머신러닝에서 중요한가?
그럼 고유값, 고유벡터가 머신러닝에서 왜 중요한걸까요?
이 값을 알게 됨으로써 데이터의 핵심을 잘 파악하고, 복잡한 문제를 쉽게 풀 수 있기 때문입니다.
예를 들어 데이터의 핵심인 나무젓가락이 있다고 해볼게요.
여러 데이터가 표현되면서 또 다른 데이터인 고무 찰흙이 나무젓가락에 덕지덕지 붙습니다. 그럼 데이터가 점점 무거워지겠죠.
그래서 데이터의 핵심만 잘 발라내는 것이 중요합니다. 이게 바로 고유 벡터를 찾는 것이라고 할 수 있죠.
간단히 말하면, 데이터의 본질적인 특징을 잘 나타내는 방향을 찾는다고 보시면 됩니다.
추후 배울 PCA(주성분 분석) 등에서 이용됩니다.
오늘은 고유값과 고유벡터에 대해 알아보았는데요!
궁금한 점 있으면 언제든지 댓글 남겨주세요!
읽어주셔서 감사합니다.

