특이값 분해 SVD는 머신러닝 공부하시는 분들은 정말 많이 들어보셨을 겁니다.
생각보다 개념이 어렵기도 하고, 보고 봐도 이해가 잘 안되는 경우가 많을겁니다.
이번 포스팅에서는 최대한 쉽게 특이값 분해에 대해 알려드리려고 하는데요.
혹시나 이해가 되지 않는다면 언제든지 댓글 남겨주세요!

특이값 분해(SVD,Singular Value Decomposition)란?
특이값 분해는 행렬을 여러 개의 작은 행렬로 쪼개서 더 쉽게 다룰 수 있도록 만드는 방법입니다.
예를 들어서 밴드 음악이 있다고 가정해볼게요. 이 밴드 음악에는 기타, 드럼, 베이스, 보컬이 하나로 섞여 만들어지죠.
근데 우리가 베이스를 연습하는 사람들이라고 한다면, 이 음악에서 베이스 소리만 똑 떼어내서 들으면 참 좋겠죠.
그럼 기타, 드럼, 보컬 소리를 제거하고, 베이스 소리만 남기게 됩니다.
이게 바로 특이값 분해인데요. 행렬을 여러개의 중요한 부분으로 쪼개서, 원하는(중요한) 정보만 남길 수 있게 해주는 방법입니다.
특이값 분해 계산 방법
특이값 분해는 아래의 식을 만족합니다.

- A : mxn 크기의 원본 행렬
- U : mxm 크기의 직교 행렬
- Σ : mxn 크기의 대각 행렬
- 𝑉^𝑇 : nxn 크기의 직교 행렬
직교, 대각 행렬이 뭔지 헷갈리시면 아래를 클릭하셔서 확인해주세요.
직교 행렬
직교 행렬은 자기 자신의 전치 행렬과 역행렬이 동일한 행렬입니다.
즉, 행렬 Q가 직교행렬이 되려면 아래의 조건을 만족해야합니다.

특징은 다음과 같습니다.
- 역행렬이 전치행렬과 같다.
- 벡터의 길이를 유지한다.
- 직교 행렬의 열과 행은 서로 직교하며, 크기가 1인 단위벡터이다.(서로 수직이며 길이가 1이다)
구체적인 예를 들자면 아래와 같은 행렬이 직교 행렬이라 할 수 있겠습니다.

대각 행렬
대각 행렬은 대각선 이외의 원소가 모두 0인 행렬입니다.
즉, 아래와 같은 형태를 만족합니다.

대각 원소는 모두 0이 아니어야합니다.
특이값 분해는 원본 행렬인 A를 좌측 특이벡터 U, 특이값 행렬 Σ, 특이 벡터 행렬 𝑉^𝑇으로 나눕니다.
이제 예를 들어서 계산을 하나씩 해볼텐데요. 차근차근 따라와주세요!
혹시나 왜 이수식이 나왔는지 이해가 안된다면, 아래에서 유도해드릴테니, 일단은 한번 읽어주세요!
A행렬은 다음과 같이 정의하겠습니다.
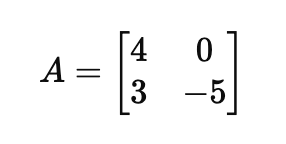
(1) A^TA와 AA^T계산


위의 과정은 고유값과, 고유벡터를 구하는 과정입니다.
(2) 특이값 Σ 구하기
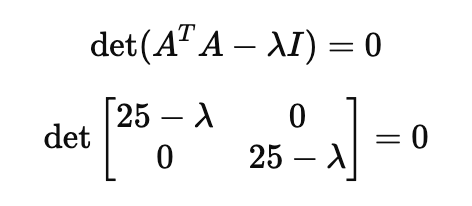
여기서 고유값을 구하면

이렇게 나오는데요.
특이값은 고유값의 제곱근으로 구할 수 있습니다.
(이것도 왜 그런지 아래에서 설명해드릴게요)

이 값으로 대각행렬인 Σ를 구할 수 있습니다.

(3) U와 V행렬 구하기
A^TA의 고유벡터를 구하면 행렬 𝑉를 구할 수 있습니다.

따라서 𝑉^𝑇는 다음과 같이 나올 수 있습니다.
AA^T를 이용하면 U벡터를 구할 수 있는데요. AA^T의 고유벡터를 계산하면 아래와 같습니다.

따라서 최종적으로는 다음과 같이 구해집니다.

특이값 분해 수식 유도
특이값 분해가 왜 저런 수식을 가지게 되었는지 직접 유도해보겠습니다.
들어가기 전 특이값 분해는 고유값 분해를 일반화한 수식이라는 것을 알아주세요!
(1) 고유값 분해
고유값과 고유 벡터는 다음과 같은 수식을 만족하는데요.

- A : nxn 크기의 정방 행렬
- v : 행렬 A의 고유벡터 (0이 아닌 벡터)
- λ : 행렬 A의 고유값 (스칼라값)
위의 조건을 만족하고, 그 의미는 행렬 A가 벡터 v에 작용했을 때, 방향은 그대로고 크기만 λ배 변한다는 것을 의미해요.
만약 고유값, 고유벡터를 모르신다면 아래 포스팅을 먼저 봐주세요!
가장 쉽게 설명하는 고유값과 고유벡터
최근 자연어 처리의 기본에 대해 포스팅을 시작했는데요.통계적 임베딩을 설명하는데 반드시 필요한 개념인데,해당 포스팅에 담기에는 또 너무 길더라고요.그래서 고유값, 고유벡터 먼저 설명
jaeyoon-95.tistory.com
만약에 행렬 A의 고유벡터가 n개 있다고 가정해 볼게요.
이 행렬을 V라고 정의하고 하나로 묶으면 아래와 같이 표현할 수 있습니다.

그럼 이제 전체 수식으로 다시 돌아와 볼게요.

이걸 행렬 형태로 한번에 정리하면 아래와 같이 수식을 정리할 수 있습니다.

그럼 위에서 정의한 V에 의해 수식을 변환할 수 있습니다.
오른쪽은 각 고유벡터에 대응하는 고유값을 곱한것이기 때문에 다음과 같이 변환 가능합니다.

이 값을 우리는 Λ로 정의해줄 수 있습니다.

V의 역행렬을 곱해주면 아래의 수식을 구할 수 있습니다.

각 행렬의 의미는 다음과 같습니다.
- V^-1 : 원래 좌표계를 "고유 벡터 좌표계"로 변환
- Λ : 고유값만큼 크기를 변환
- V : 다시 원래 좌표계로 돌림
의미를 한번 정리해보면 고유값 분해라는 것은 행렬을 고유벡터와 고유값을 이용해 분해하는 방법입니다.
고유벡터 행렬 V를 이용해 원래 행렬을 변환한다면, 단순한 대각행렬인 Λ으로 표현할 수 있습니다.
즉, 위의 수식을 통해 "축을 따라 크기만 변하는 연산"으로 해석될 수 있다는 이야기죠!
그럼 이게 왜 특이값 분해랑 연관이 있는 걸까요?
기존 고유값 분해는 행과 열의 크기가 같은 정방행렬에서만 적용이 가능합니다.
즉, 직사각형(비정방) 행렬에서는 적용할 수 없다는 단점이 있어요.
그래서 더 일반적인 방법인 SVD가 필요하게 되었습니다.
(2) 일반적인 고유값 분해 SVD
위에서 SVD는 직사각 행렬도 가능하게 만든다고 말씀드렸습니다.
사실 수식 자체가 정사각 행렬 계산으로 되기 때문에, 한 번에 직사각 행렬로 계산하게 된다면, 수정되는 부분이 굉장히 많을텐데요.
그래서 우리는 직사각 행렬 A를 아래와 같이 만들어줄 수 있어요.

A가 mxn크기를 가진다고 하면, nxm크기를 가지는 A^T를 곱해줄 때 mxm, 혹은 nxn크기를 가지게 됩니다.
그렇다면 이 값은 정방행렬이 되겠죠!
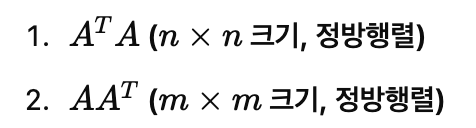
그럼 위에서 알게된 고유값 분해 수식에 대입할 수 있게 됩니다.
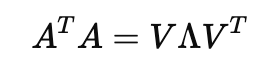
V, Λ 값은 이렇게 정의할 수 있게 됩니다.
- V : A^TA의 고유벡터 행렬
- Λ : A^TA의 고유값 행렬
반대로 AA^T도 대입해 줄 수 있는데요.

U, Λ값은 이렇게 정의할 수 있게 됩니다.
- U : AA^T의 고유벡터 행렬
- Λ : AA^T의 고유값 행렬
위의 수식에서 보면 고유 벡터 행렬은 다르지만, 고유값 행렬은 동일한 것을 확인할 수 있는데요.
이것은 아래 펼치기에서 상세하게 확인하실 수 있어요.
먼저 A^TA의 고유값과 고유벡터 수식 정의를 하면 다음과 같습니다.

이제 왼쪽에 A행렬을 곱해주겠습니다.
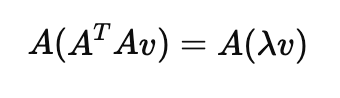
이를 새로 정리하면 아래와 같이 할 수 있습니다.
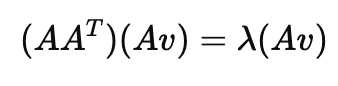
여기서 Av를 새로운 벡터라고 정의한다면, AA^T에 대한 고유값, 고유벡터 정의가 가능해집니다.
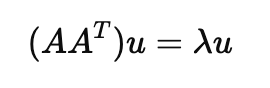
λ는 모든 식에서 동일하게 등장하는 것을 알 수 있죠.
따라서 AA^T, A^TA의 고유값은 동일하다고 할 수 있습니다.
SVD설명할 때 "특이값은 고유값의 제곱근으로 설정한다"라고 말씀드렸는데요.
특이값은 실제 변형된 크기를 나타내야하는데, 우리가 정방행렬로 만들려고 AA^T, A^TA처럼 A행렬을 두 번 곱해줬습니다.
따라서 원래 크기를 알고싶다면 제곱근을 취해줘야합니다.
아래와 같은 수식을 얻을 수 있습니다.

이제 원래 행렬인 A를 위에서 구했던, U, V, Σ로 표현해 보겠습니다.
A^TA의 고유값과 고유벡터 수식을 적용시켜볼게요.

이제 양 변에 A를 곱해보겠습니다.

λ는 스칼라이기 때문에 다음과 같이 앞으로 뺄 수 있습니다.

그럼 다음과 같은 수식이 만들어집니다.
왜 두 행렬의 고유값이 같은지 증명할 때와 비슷한 유도식이 나오게 됩니다.

위의 식을 보면 Avi자체를 하나의 벡터로 보면, AA^T의 고유벡터라고 할 수 있습니다.
그럼 AA^T의 고유벡터는 ui이기 때문에, Avi는 ui의 배수 형태가 됩니다.
아래와 같이 수식을 적어줄 수가 있겠네요.

여기서 c값은 특이값인 Σ으로 바꿔주시면 됩니다. 왜 바꿔주는지는 위에서도 말씀 드렸습니다.(=원래 크기를 알고싶기 때문)

그럼 이렇게 표현이 가능하겠죠!
양 변에 V^-1를 곱해주면 우리가 알고있는 특이값 분해의 식이 완성됩니다.

각 행렬의 의미
특이값 분해가 나누는 것은 알겠는데, 각 행렬이 어떤 의미를 가지는지 궁금하시죠?
아래서 하나씩 알려드릴게요!
U 행렬이 가지는 의미
A행렬이 가진 기본적인 패턴을 나타내는 행렬입니다. U의 각 열은 A의 특징 패턴을 나타내는 벡터입니다.
Σ행렬이 가지는 의미
A행렬이 가진 중요한 정보의 강도를 나타내는 행렬입니다. 숫자가 클수록 중요한 정보입니다.
Σ는 대각행렬인데, 대각선에 특이값이 들어갑니다. 특히 데이터를 압축할 때 많이 사용됩니다.
𝑉^𝑇행렬이 가지는 의미
A행렬이 어떤 방향을 가지고 있는지 나타내는 행렬입니다.
𝑉^𝑇의 행은 A의 원본 데이터가 어떤 방향으로 변하는지를 나타냅니다.
이번 포스팅에서는 특이값 분해 SVD에 대해 알아봤습니다!
살짝 어려우실 수 있는데요!
이해 안되시면 댓글로 질문남겨주세요~!

'인공지능공부 > 인공지능기본지식' 카테고리의 다른 글
| [AI 기본 지식] 손실함수의 모든 것 (0) | 2023.03.22 |
|---|---|
| [AI 기본 지식] 역전파의 모든 것 (4) | 2021.04.16 |
| [AI 기본 지식] 최적화 함수의 모든 것(2) (0) | 2021.04.16 |
| [AI 기본 지식] 최적화 함수의 모든 것(1) (1) | 2021.04.16 |
| [AI 기본 지식] 활성화 함수의 모든 것 (0) | 2021.04.16 |
